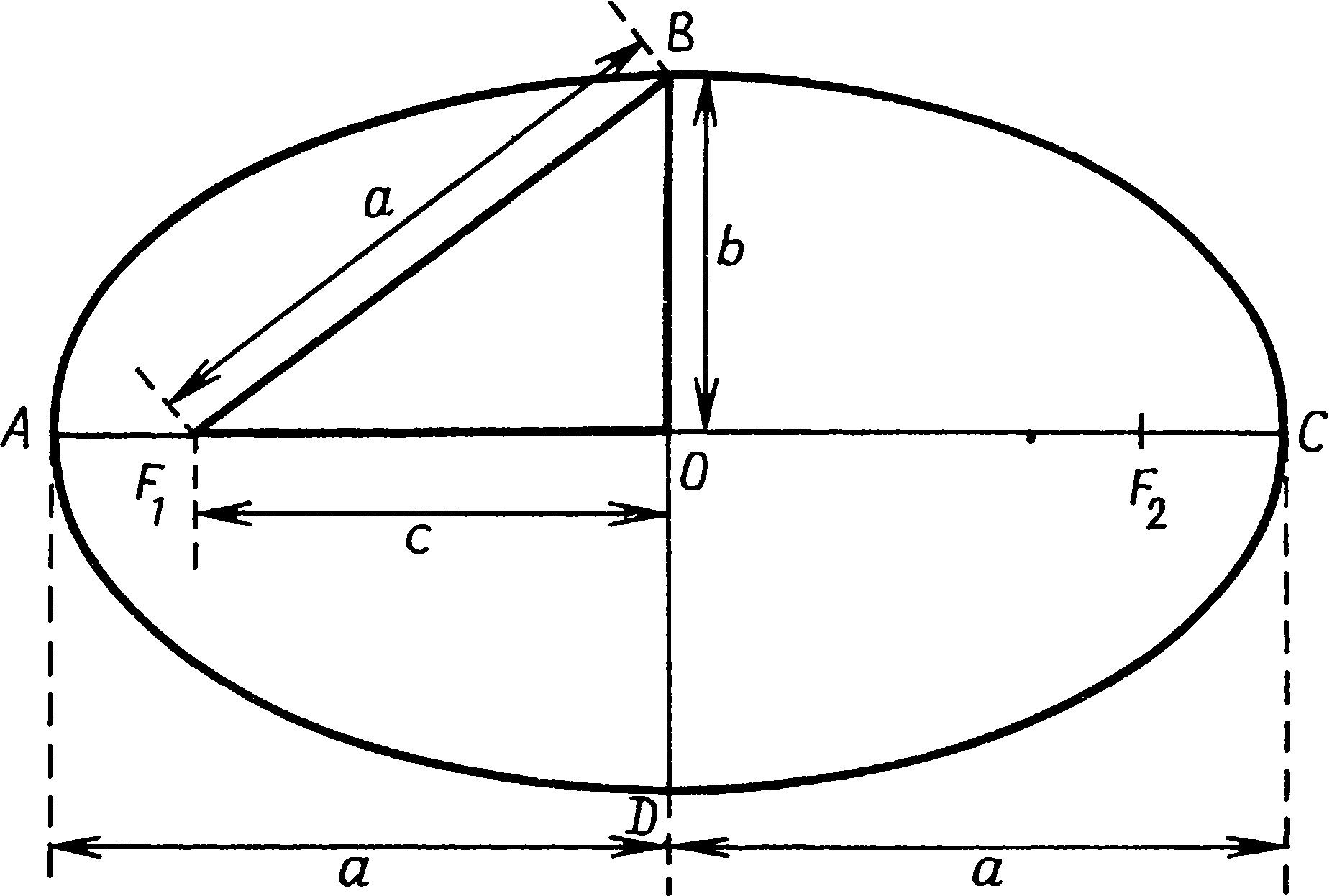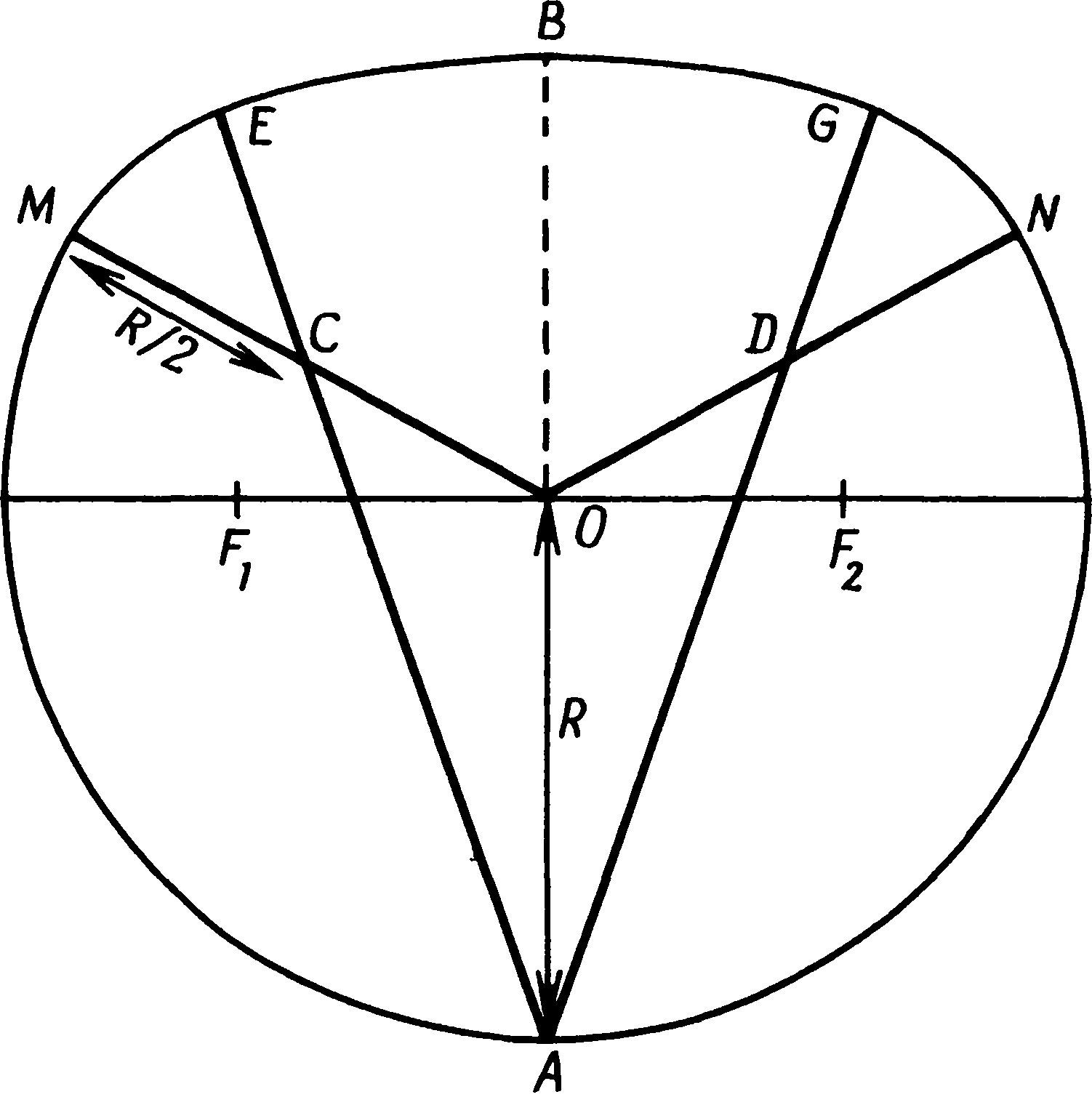
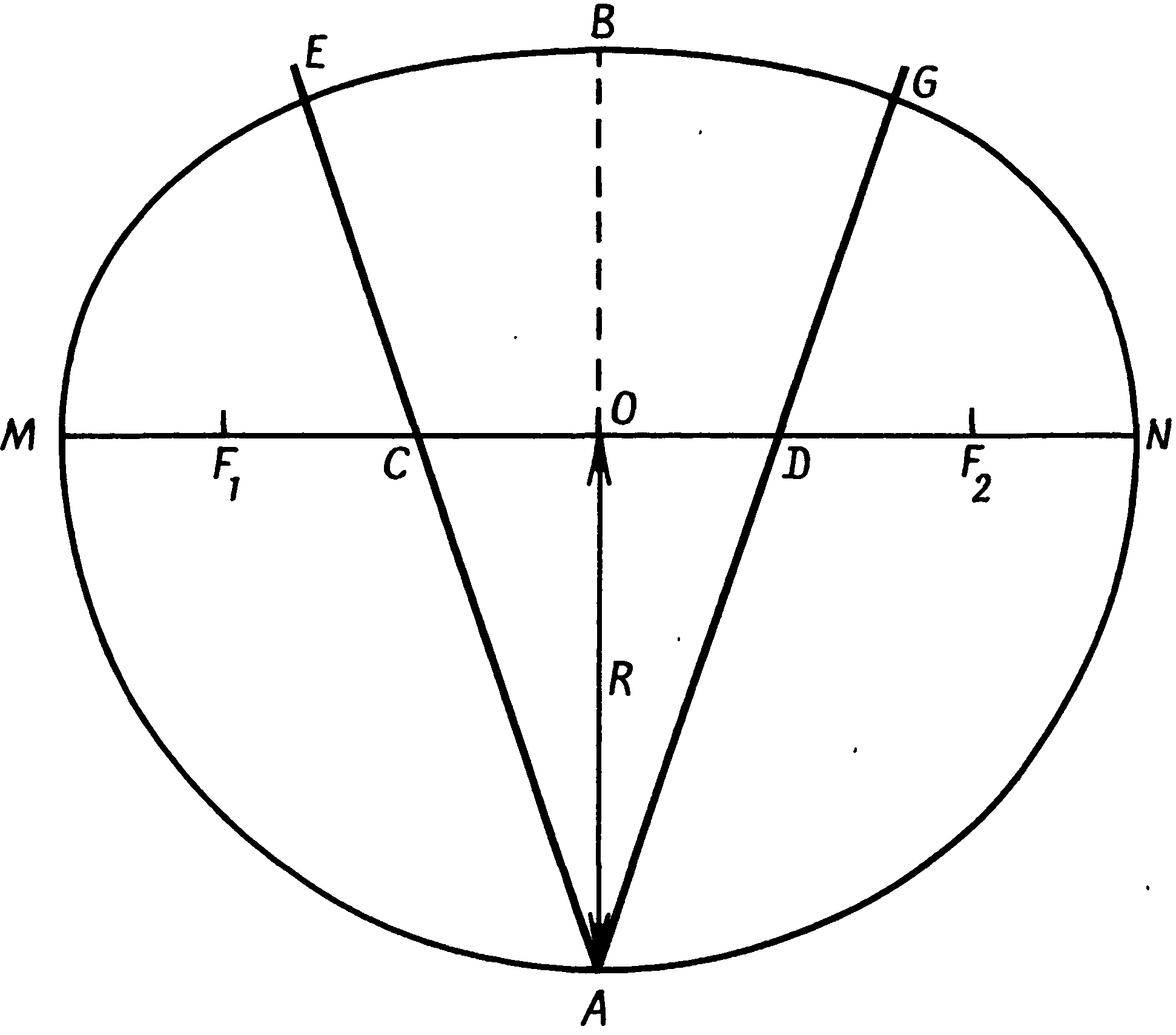
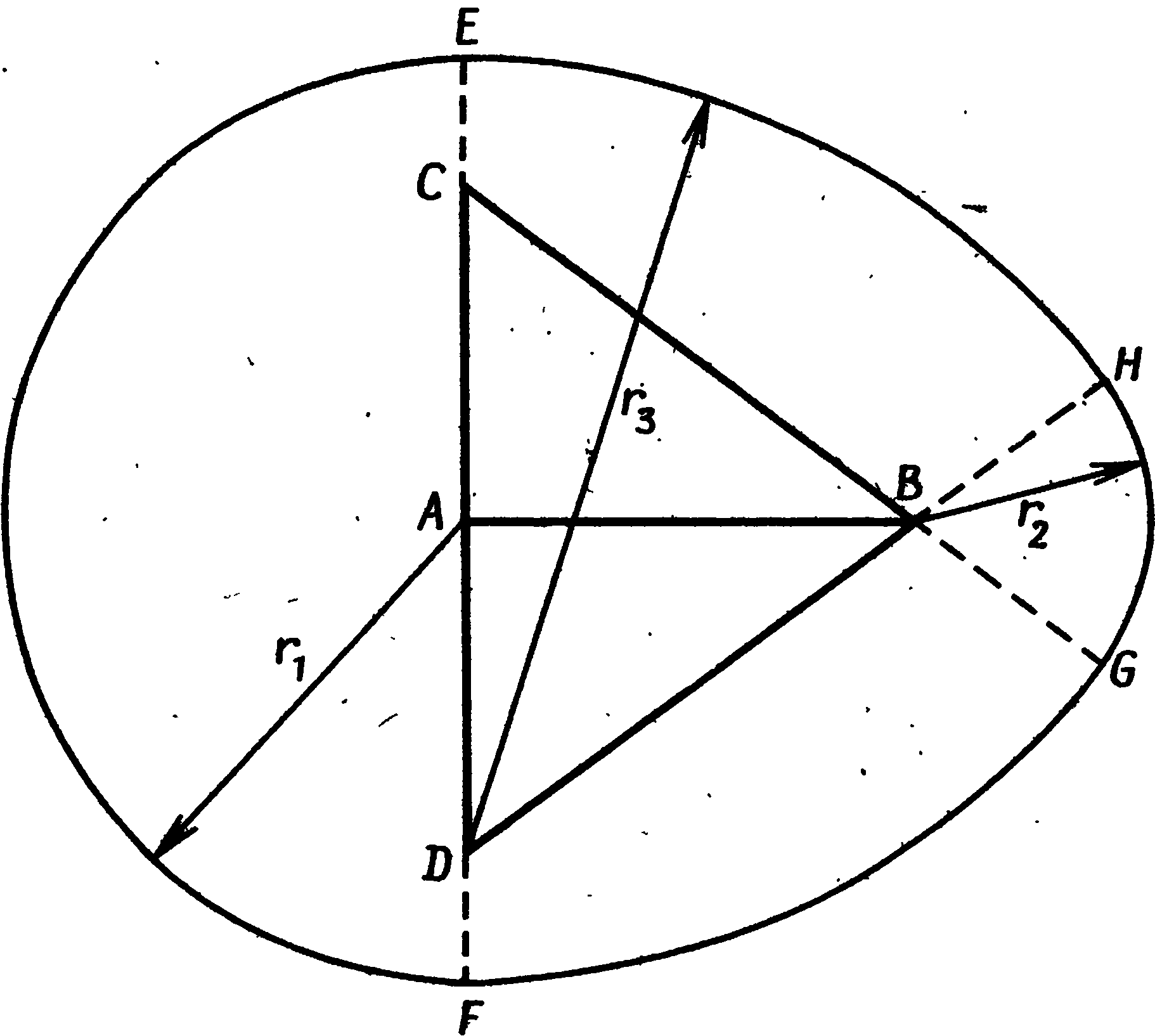
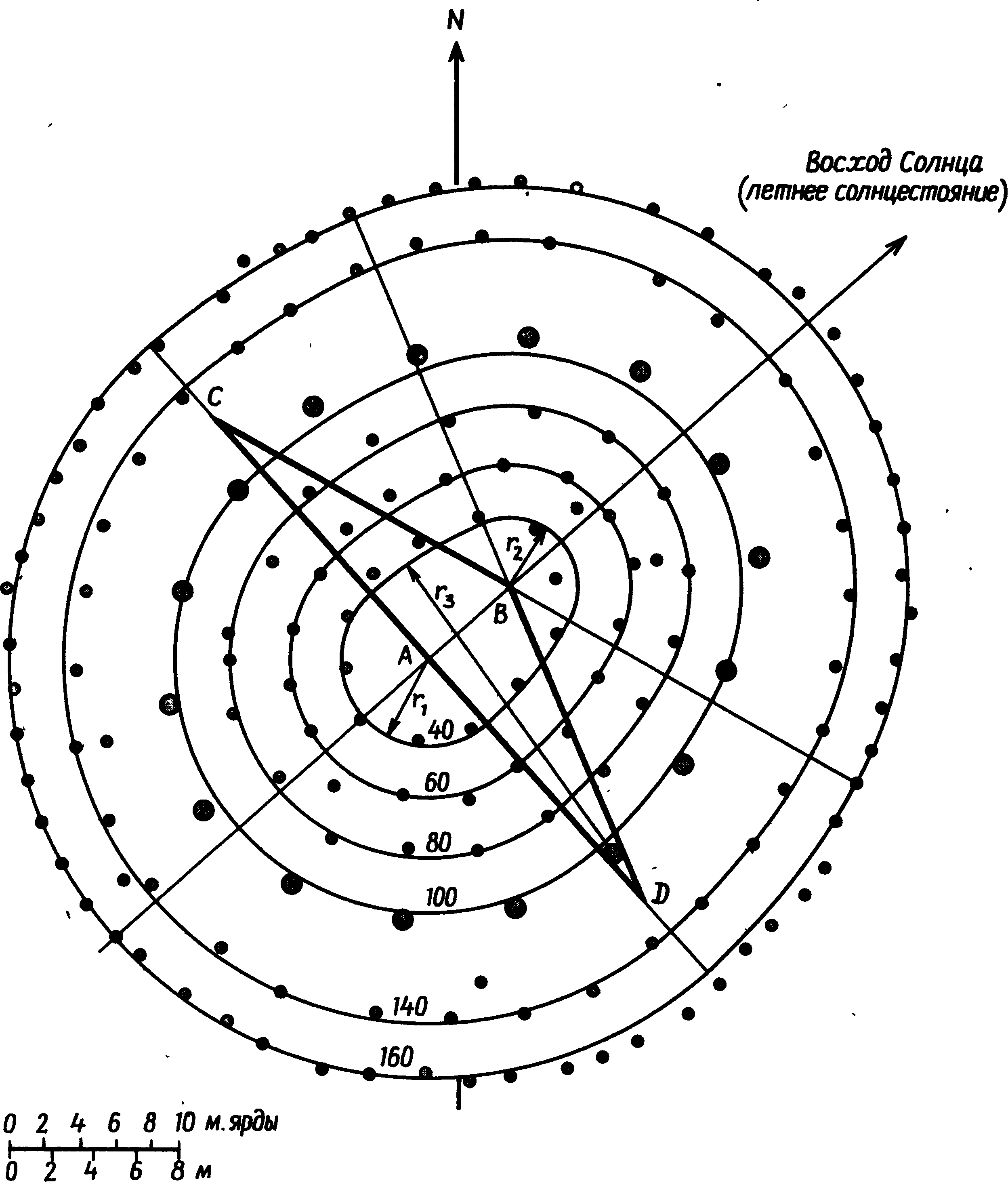
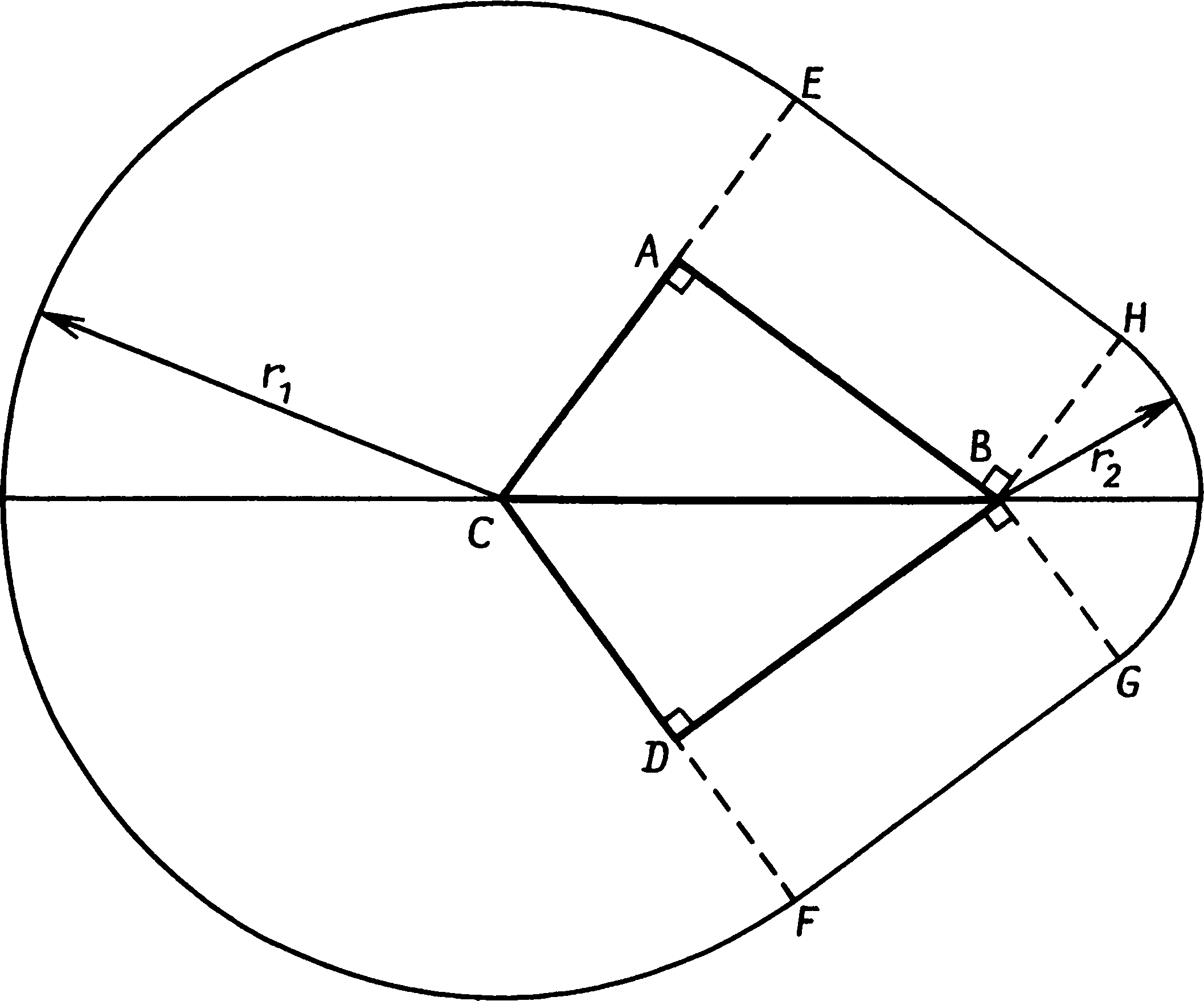
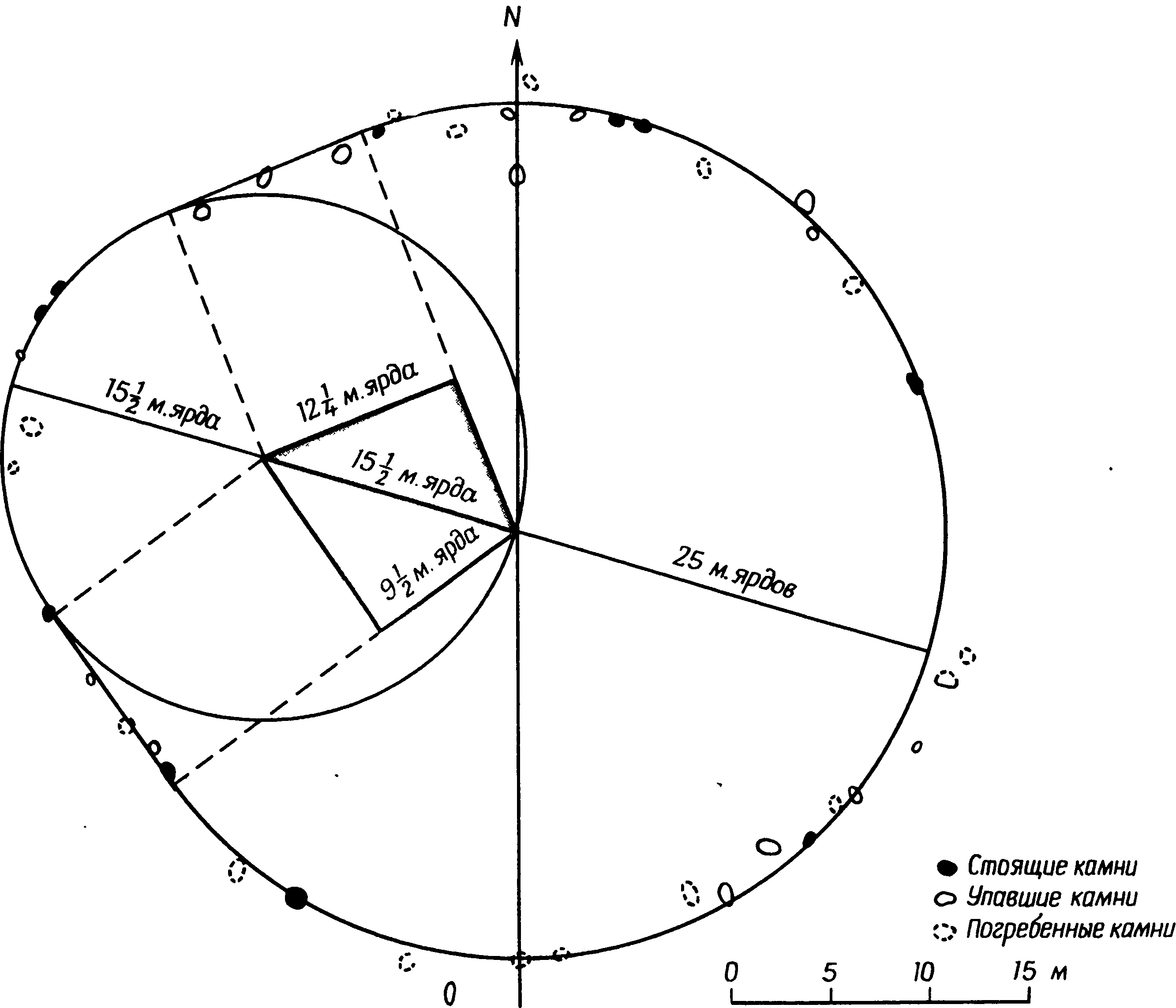
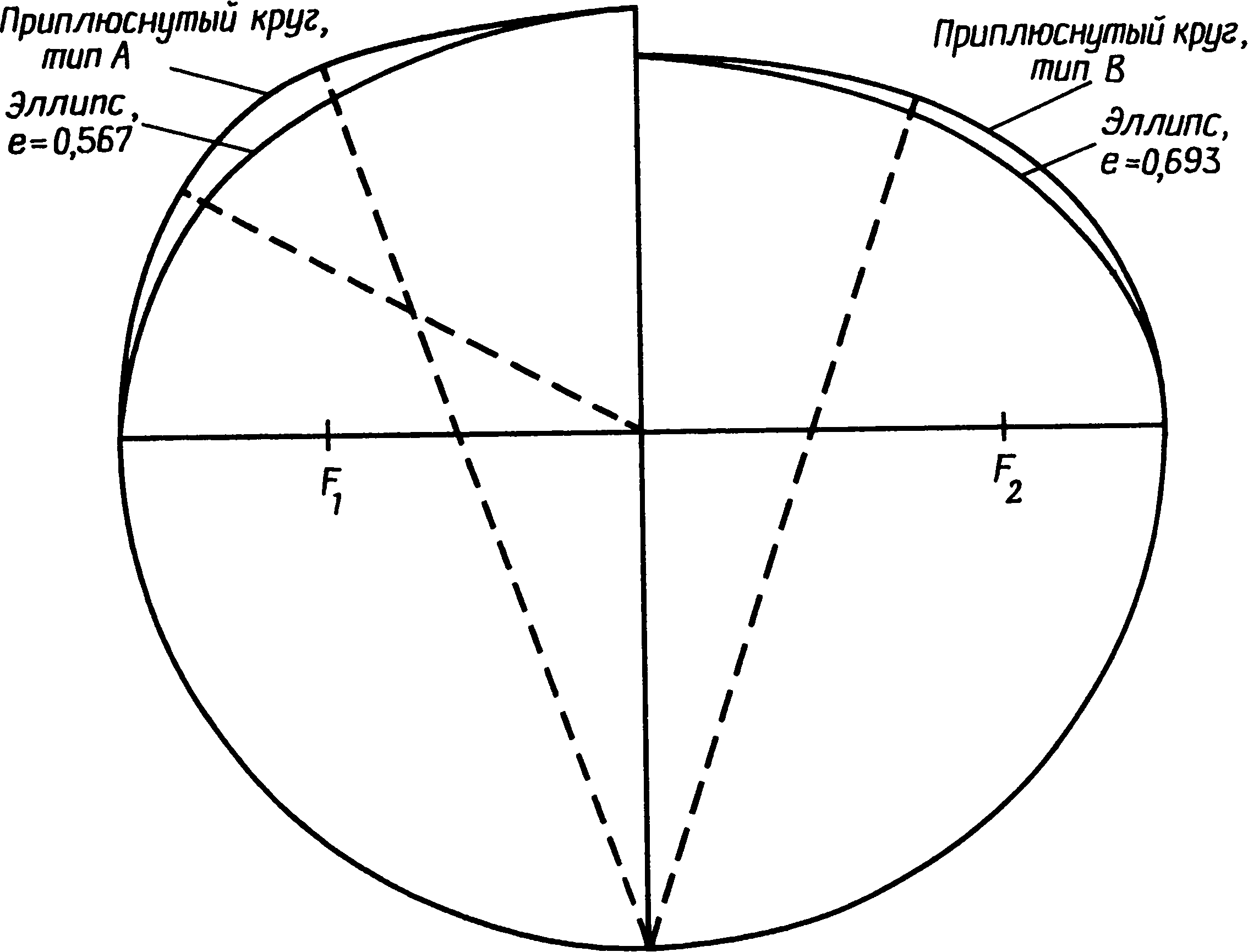
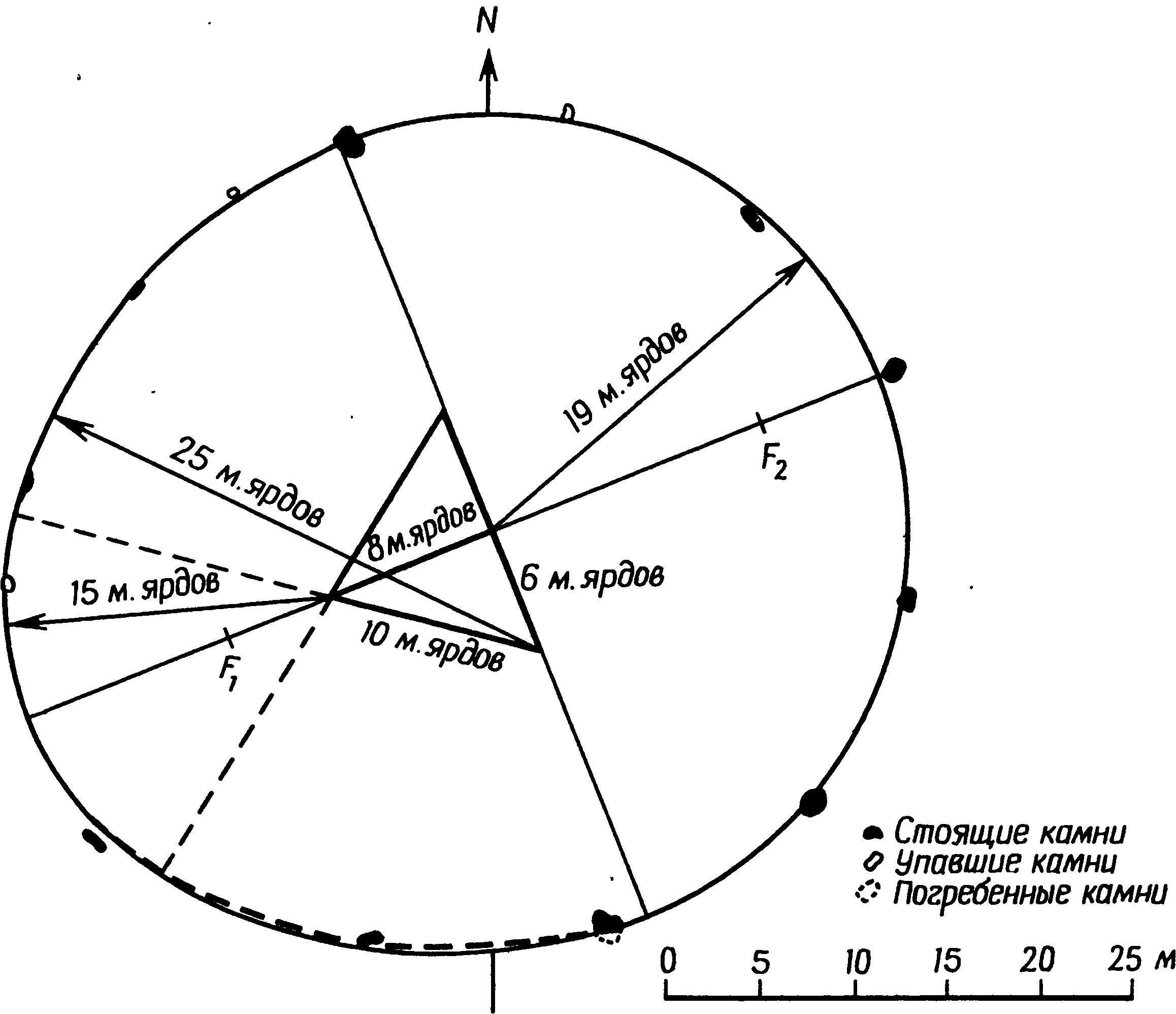
3. Мегалитическая математика

Обращаясь к вопросу о математике в неолите и раннем бронзовом веке, следует соблюдать особую осторожность. Затруднения возникают не только из-за отсутствия документальных свидетельств, но и из-за разрывов в культурной традиции. Единственное, что могло бы нам помочь, — это еще сохранившиеся памятники, но и они в подавляющем большинстве случаев повреждены, неполны или даже частично «реставрированы» любителями старины в те времена, когда еще не существовало современных методов научного анализа. Мы смотрим на эти памятники глазами людей XX в. и легко можем поддаться соблазну увидеть в них отражение наших собственных представлений о пространстве, времени, религии и космологии. Наше общество по разным экономическим и социальным причинам нередко предпочитает сложные методы организации или строительства более простым, и мы полностью забываем о том, что умели делать люди до начала промышленной эры. А если и вспоминаем, то далеко не всегда отдаем себе отчет, насколько эффективно они справлялись со стоявшими перед ними задачами.

В доказательство можно привести пример чрезвычайно простого разрешения, казалось бы, очень трудной проблемы — правда, дело происходило не совсем в ту эпоху и далеко от тех мест, которые мы рассматриваем в этой книге. Прежде чем укладывать первые ряды камней в основание пирамиды, египтяне должны были выровнять под него достаточно большую площадку. Стороны пирамиды Хеопса в Гизе имеют длину 230 м, и площадка была подготовлена с такой точностью, что перепад высот в крайних точках составлял менее 2 см. Остановитесь на минуту и попробуйте сообразить, как удалось добиться этого не только без современных геодезических инструментов, но, собственно говоря, и вообще без всяких измерительных приспособлений. Египтяне поступили так: они обнесли площадку земляной дамбой, залили ее водой и оставили воду испаряться. Едва в этом искусственном озере появлялись острова, их срезали, пока вся площадка не была выровнена с необходимой точностью.

Насколько нам известно, этот прием на северо-западе Европы никогда не применялся, и мы напомнили здесь о нем просто для того, чтобы показать, насколько может быть эффективен простой метод, даже если задача представляется на первый взгляд очень сложной. Рассматривая мегалитические памятники, следует начинать с вопроса: «Какой минимум технических знаний требовался для такой работы?», а затем старательно отделять факты от предположений. На такой основе мы сможем определить вероятные или хотя бы возможные пределы знаний мегалитических математиков.

Не так-то легко преодолеть в себе привычные стереотипы современного мышления. Мы пользуемся математическими моделями, которые опираются на открытия многих великих ученых от Евклида до Эйнштейна. Нам известны методы индуктивной логики, т.е. методы выведения одного факта из другого путем последовательных многоступенчатых рассуждений. Они преподаются в школе и используются, например, для доказательства геометрических теорем о подобии треугольников и многих других. Мы, кроме того, учимся символической логике и применяем ее в алгебраических уравнениях, манипулируя выражениями, содержащими и буквы, и числа. Это весьма действенные способы решения задач, и после некоторой практики они становятся привычными, само собой разумеющимися, и иной раз заставляют нас забыть тот факт, что многие задачи можно решить — хотя бы приближенно — и без них.

Нет никаких оснований думать, будто люди неолита и раннего бронзового века располагали какими-нибудь современными математическими знаниями, но трудно не признать их увлечения геометрией. Хотя спирали, полукружья и другие фигуры на стоячих камнях и в могильниках также свидетельствуют о таком интересе, наиболее явное его доказательство дает нам изучение каменных кругов и колец. Нередко это — правильные круги, аккуратно размеченные и аккуратно построенные, но другие представляются кругами только на первый взгляд, а при точной съемке оказываются совсем иными фигурами. Но это отнюдь не результат небрежной мегалитической работы. Такие каменные кольца бывают иногда хорошо вычерченными эллипсами, и очень часто это — модифицированные круги, либо сознательно уплощенные, так что фигура напоминает слегка приплюснутый апельсин, либо вытянутые, как яйцо. Внимательное рассмотрение этих фигур дает несколько неожиданные результаты, поскольку они обладают интересными математическими свойствами, которые вряд ли можно объяснить случайностью.

Первым ученым, указавшим на сложность мегалитической геометрии, был профессор Том. В своих печатных работах он объясняет сделанные им открытия современным научным языком и, демонстрируя геометрические отношения, заложенные в каменных кольцах, пользуется современными математическими методами. К несчастью, многие его читатели решили, что такое же знание математики было необходимо и для того, чтобы создать эти формы при постройке каменных колец. Принять подобную идею они не могли, а потому скептически отнеслись к самим фигурам, образованным камнями, считая, что исследователи

склонны приписывать им крайне глубокие и тонкие истолкования, которые ничего общего с действительностью не имеют. Эти критики упустили из виду, что даже очень сложные фигуры можно создавать с помощью самых простых методов.

Примером фигуры, которую гораздо легче нарисовать, чем описать математически, может послужить спираль. Каменные кольца не строились по спиралям, но эта фигура часто встречается в орнаментах, вырезанных на камнях. Хотя математическое уравнение для спирали с постоянным шагом не очень сложно, понимание его требует знания аналитической геометрии, которую преподают только в старших классах школы. Однако нарисовать такую спираль очень просто. Возьмите кол, вбейте его в землю и привяжите к нему веревку так, чтобы она по нему не скользила. К другому концу веревки привяжите заостренный колышек и идите вокруг кола так, чтобы веревка наматывалась на него, держа ее все время натянутой. Острый колышек вычертит на земле спираль, витки которой постепенно будут становиться все меньше, пока веревка не намотается вся. Человек, начертивший таким способом спираль, может не иметь ни малейшего представления о ее математических свойствах — о том, что с каждым оборотом ее диаметр уменьшается на одну и ту же величину, что расстояние между витками равно длине окружности центрального кола, что касательные к спирали в любой точке образуют постоянный угол с ее радиусом, — однако она все равно будет обладать этими свойствами. Мораль: если в памятнике обнаруживаются какие-то математические свойства, остерегайтесь делать из этого вывод, будто строители о таких свойствах знали и намеренно воплотили их в своем сооружении.

Хотя существуют и другие варианты, правильный круг — это наиболее обычная форма каменных колец, и встречается она много чаще остальных. На протяжении всего своего долгого развития Стоунхендж сохранял форму круга, возникшую еще при постройке земляного вала первоначального хенджа. Лунки Обри были расположены по окружности радиусом 43,2 м, и 1800 лет спустя эта фигура была повторена, когда сарсеновое кольцо было построено по кругу радиусом 14,79 м, хотя новый центр сместился на 0,55 м к северу.

Важно установить, какой точности могли добиваться строители каменных колец. Мы уже упоминали утверждения критиков, что у них не было математических знаний, необходимых для создания более сложных фигур, чем круг. Другие критики указывали, что у них не было технических возможностей для установки камней с той точностью, какой добиваются современные геодезисты. Однако все как будто соглашаются, что круги строились сознательно, а потому, если мы установим, насколько они точны, это поможет нам разобраться в более сложных фигурах.

Кольцо лунок Обри недавно было нанесено на план с большим тщанием. Края лунок были определены с помощью внимательного зондирования, а центры отмечены металлическими колышками. Круг оказался поразительно точным. Ошибка в расположении центров лунок составляет около 0,17 м (строго говоря, 0,17 м — это среднеквадратическое уклонение). Такая ошибка составляет примерно 0,4% радиуса. Труднее оценить точность сарсенового кольца, так как все его камни, кроме трех, в то или иное время передвигались. Однако вогнутость, приданная их внутренним поверхностям, чтобы они следовали кривизне круга, показывает, что строители стремились достичь высокой точности.

Важный мегалитический памятник на самом севере Британских островов — Кольцо Бродгара на Мейнленде, крупнейшем острове Оркнейской группы, — представляет собой правильный круг из 58 камней радиусом 51,83 м. От части камней остались только их основания. Из всех 58 камней лишь 9 отстоят от линии окружности более чем на 0,5 м и лишь два отодвинуты от нее более чем на метр. К сожалению, в XIX в. некоторые камни были установлены заново, а другие отклонились от вертикали, так что первоначально Кольцо Бродгара было, вероятно, построено с большей точностью, чем это можно заключить по его теперешним остаткам. Без раскопок, которые позволили бы найти первоначальные ямы сомнительных камней, невозможно судить, какой степени точности удалось достичь строителям. Мы можем сказать только, что большинство камней было установлено не далее полуметра от линии окружности. (Если включить в расчеты все камни, то среднеквадратическое уклонение составит 0,55 м, если же исключить два сильно сдвинутых камня, оно сокращается до 0,4 м.) Точность не так велика, как достигнутая в Стоунхендже, когда размечалось кольцо лунок Обри, и тем не менее в Бродгаре отклонения не превышают 1% радиуса. Круги в Стоунхендже и в Бродгаре свидетельствуют о том, что мегалитические инженеры прекрасно умели строить правильные каменные круги, и потому представляется правдоподобным, что там, где эта форма не соблюдена, они отступали от нее сознательно.

Для того чтобы простейшим способом разметить на земле каменный круг, требуется в первую очередь веревка или ремень вдвое длиннее радиуса предполагаемого круга. Веревка складывается пополам и накидывается на крепко вкопанный в землю столб, а к свободным концам привязывается острый кол, которым и чертят по земле. Чтобы нарисовать круг, надо обойти центральный столб, все время туго натягивая веревку. Петля удобнее простой веревки, особенно если столб неотесан, так как она легче скользит по нему.

Аккуратно нарисовать большой круг с помощью веревки совсем не легко. Прежде всего, если изменять приложенное к веревке усилие, она растягивается, и чем она тоньше, тем больше возможность ее удлинения. Поэтому более предпочтительна толстая и крепкая веревка, но с ней труднее работать. Есть и еще одна трудность: длина и растительных волокон, и ремней меняется, когда они отсыревают. Если разметка будет начата в сырое росистое утро и затянется до времени, когда солнце высушит росу, длина мерной веревки изменится. Строители могли справиться с такой трудностью, часто проверяя длину веревки по первому колышку, которым они отметили в этот день расстояние от центра до окружности. И наконец, на точности могут сказаться неровности почвы, а чтобы избежать ошибки из-за провисания веревки, несколько человек, возможно, поддерживали ее в горизонтальном положении.

Рис. 3.1. Геометрия прямоугольного треугольника. AC2 + AB2 = BC2, или b2 + c2 = a2.

Прежде чем заняться описанием каменных колец, не имеющих точной формы круга, посмотрим, как могли люди раннего бронзового века строить прямоугольные треугольники. Современные школьники изучают одно из самых знаменитых открытий классической геометрии — теорему Пифагора, гласящую, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. На рис. 3.1 треугольник ABC иллюстрирует эту теорему: если A — прямой угол, то AB² + AC² = BC². Наиболее известный пифагоров^* треугольник имеет стороны, равные 3, 4 и 5 единицам длины, и он действительно прямоугольный, так как 3² = 9, 4² = 16, а 9 + 16 = 25 = 5².

Такой треугольник — простейший прямоугольный треугольник, отношение трех сторон которого выражается небольшими целыми числами. Люди раннего бронзового века, несомненно, были с ним знакомы. Этот треугольник вновь и вновь повторяется в каменных сооружениях той эпохи. Иногда он положен в основу формы каменных колец и довольно часто определяет взаимное положение нескольких каменных колец или отдельных стоячих камней данного памятника. Мегалитические геометры, по-видимому, знали, что этот треугольник обладает особыми свойствами.

Существуют и другие пифагоровы треугольники, отношение сторон которых выражается большими целыми числами — например, 5:12:13, 8:15:17, 7:24:25, 20:21:29 и 12:35:37. Не все эти треугольники были обнаружены в мегалитических памятниках, однако самый большой — с отношением сторон 12:35:37 — их строители знали и использовали, а потому не исключено, что еще будут обнаружены памятники, в основу которых положены и остальные перечисленные треугольники.

В некоторых памятниках использовались не истинные, а приближенные пифагоровы треугольники — например, с отношением сторон 8:9:12. В этом случае 8² + 9² = 145, тогда как 12² = 144. Угол между двумя короткими сторонами равен у такого треугольника 89,6 вместо 90°, и сомнительно, чтобы столь незначительное отклонение могло быть замечено. В более близкие к нам времена плотники пользовались в сочленениях крыш треугольником с отношением сторон 10:10:14, который дает угол 88,8° — тоже приближенный, но еще менее точный. Однако все указания на использование этих треугольников ре дают нам права утверждать, будто теорема Пифагора была открыта уже в бронзовом веке. Наоборот, в связи с использованием приближенных пифагоровых треугольников можно предположить, что математические отношения сторон открыты не были, но строители чисто эмпирически отобрали типы треугольников, позволявших без труда размечать на земле прямые углы. Случайно обнаружив, что некоторые треугольники образуют прямые углы, они запомнили длину их сторон и использовали их снова и снова.

Способ построения прямого угла крайне прост: надо разложить на земле веревочный треугольник со сторонами выбранной длины, натянув их как можно туже. Еще большей точности можно достичь с набором жердей одинаковой длины, сделав, например, одну сторону из трех таких жердей, уложенных конец в конец, вторую — из четырех, а третью — из пяти. Естественно, что чем длиннее жерди, тем точнее будет окончательный результат. Примеры использования прямоугольных треугольников мы встретим, когда перейдем к каменным кольцам, не имеющим формы правильного круга.

Следующей после круга наиболее простой фигурой является эллипс. Его можно рассматривать как круг с двумя центрами. Если вкопать в землю два столба и захлестнуть их одной свободной петлей, то кол, вставленный в эту петлю, вычертит эллипс. Чем дальше отстоят друг от друга столбы, тем более вытянутым он будет. В математике точки, где помещены столбы, называются фокусами эллипса — на рис. 3.2 фокусы находятся в точках F₁ и F₂. Расстояние AC называется большой осью эллипса, а расстояние BD — малой его осью. Отношение F₁F₂/AC — это так называемый эксцентриситет эллипса; его максимальное значение может достигать 1 (эллипс при этом вытягивается в прямую линию), а минимальное — 0 (тогда эллипс превращается в окружность). Эксцентриситет мегалитических эллипсов обычно колеблется от 0,3 до 0,7. Обнаружено более двадцати каменных эллипсов, в том числе каменные кольца Постбридж в Девоншире (наименее вытянутое с эксцентриситетом всего 0,29), Пенменмаур в Гвинедде (эксцентриситет 0,31, фото IX) и Махри-Мур на острове Арран (эксцентриситет 0,5), из чего следует, что они были географически широко распространены. Относительно еще двух десятков колец пока не доказано, являются они правильными эллипсами или нет — то ли потому, что камни были передвинуты, то ли потому, что съемки их проводились недостаточно точно.

Очень соблазнительно порассуждать о том, каким образом эллипс был вычерчен впервые. Если круги вычерчивались с помощью веревочной петли, как это описано выше, он мог быть открыт совершенно случайно. Почти наверное в какой-то момент петля захлестывалась за то или иное препятствие — за камень, за пень или даже за ногу зрителя. Получившаяся при этом фигура могла показаться строителям каменных кругов настолько интересной, что они начали делать опыты с вычерчиванием эллипсов.

Одно из свойств эллипсов заключается в том, что расстояние BF₁ равно половине большой оси. На рис. 3.2 длина отрезка OB равна b, длина OA равна a, а расстояние от центра до фокусов есть с. В этих обозначениях F₁B = a. (Доказательство вытекает непосредственно из способа вычерчивания эллипса. Когда кол находится в точке A, петля тянется от F₂ до A и обратно до F₂; следовательно, ее длина равна 2a + 2c. Когда кол находится в точке B, петля охватывает вокруг F₁, F₂ и B; ее длина равна 2BF₁ + 2c. Отсюда, вычитая одно выражение из другого, получаем BF₁ = a.)

Треугольник BOF₁ прямоугольный, и если строители колец интересовались треугольниками, нет ничего удивительного в том, что в основе мегалитических эллипсов лежат пифагоровы треугольники. Таких эллипсов, собственно говоря, не очень много. Треугольник с отношением сторон 3:4:5 является основой одного из эллипсов в Калленише, два эллипса Стентон-Дрю в графстве Сомерсет основаны на треугольнике с отношением сторон 5:12:13, а треугольник типа 12:35:37 мы находим в эллипсе Давиота близ Инвернесса. Несколько эллипсов основаны на треугольниках, близких к пифагоровым — например, еще один эллипс Каллениша включает в себя треугольник с отношением сторон 7:11:13 (7² + 11² = 170, 13² = 169). Тем не менее в основу большинства мегалитических эллипсов не положены треугольники, отношения сторон которых выражаются в целых числах. Профессор Том высказал несколько предположений относительно того, почему были выбраны именно такие размеры эллипсов, и мы еще вернемся к этому ниже.

Рис. 3.2. Геометрия эллипса

Помимо кругов и эллипсов, мегалитические строители изобрели два вида приплюснутых кругов и две яйцевидные фигуры. Приплюснутые круги встречаются относительно часто. Профессор Том разделил их на тип А и тип Б; они показаны на рис. 3.3 и 3.4. В основе своей они очень похожи — в том смысле, что и тот и другой составлены из дуг окружностей с тремя разными радиусами. Тип Б (рис. 3.4) более прост: он составлен из полуокружности радиуса OA, двух сегментов окружностей радиуса CM с центрами в C и D и наконец соединяющей их дуги радиуса AE с центром в A. Вторичные центры C и D оба лежат на диаметре MN и на расстоянии одной трети основного радиуса R от центра O. Как можно построить такую фигуру, не зная классической геометрии?

а. Начертите полный круг с помощью петли, вращающейся вокруг столба O.

б. Вбейте столб в какой-либо точке окружности, например в точке A.

в. Постройте прямой угол к линии OA в точке O и проведите линию MN, перпендикулярную AO. Сложив веревку втрое, найдите точки C и D и вкопайте там еще два столба.

г. Теперь возьмите еще одну веревочную петлю и захлестните ее за столб A так, чтобы оба свободных ее конца были заведены за столб C и ее длины хватило, чтобы дотянуть их до точки M.

д. Прикрепите маркировочный кол к петле и проведите его так, чтобы он сначала начертил дугу с центром в C, а затем, когда веревка сойдет со столба C, он начал чертить дугу круга радиусом AE.

е. Продолжайте чертить дугу до точки G (следя, чтобы веревка не зацепилась за столб O), а затем пусть веревка ляжет на столб D, чтобы закончить дугу GN.

Существуют варианты этого метода, даже не требующие использования двух веревочных петель. Столбы O, A, C и D можно разместить с помощью измерительных реек, так что построение может быть сведено к этапам «г» — «е» без вычерчивания первого круга. Когда вся приплюснутая часть будет закончена, можно поместить столб в точку B, просто продлив линию AO. Затем, чтобы начертить остальную часть круга, накиньте петлю на B и, перегибая ее через столб O, проведите дугу MAN.

Рис. 3.3. Приплюснутый круг, тип А. Точки F1 и F2 не участвуют в построении этого круга, но они являются фокусами эллипса, который ближе всего совпадает с некруговой частью фигуры (см. рис. 3.9)

Известно более десятка каменных колец такого типа, включая каменное кольцо Двенадцать Апостолов около Холивуда в графстве Дамфрис, знаменитую Длинную Мег и Ее Дочек (кольцо в графстве Камберленд) и каменное кольцо в Мерривейле (Девоншир).

Приплюснутый круг типа А отличается от круга типа Б тем, что вторичные центры лежат у него не на диаметре основного круга, а на середине двух радиусов, разделенных углом 120° (рис. 3.3). После того как круг начерчен и в точке A вбит столб, наметить эти центры не составляет никакого труда. Той же веревочной петлей, которая использовалась для основного круга, можно разделить окружность на шесть частей (точно так же, как мы с помощью циркуля рисуем цветок), и это даст нам положение точек M и N. Разделив OM и ON пополам, находим точки C и D; в землю вкапываются еще два столба, и приплюснутый круг завершается так же, как для круга типа Б — вторая петля перекидывается от A через C к M.

Рис. 3.4. Приплюснутый круг, тип Б. Точки F1 и F1 не связаны с построением приплюснутого круга, но они являются фокусами эллипса, который ближе всего совпадает с некруговой частью фигуры

Этот круг тоже можно построить другим способом, используя только одну веревку. Сначала надо с помощью веревок или жердей построить равносторонний треугольник. Два равносторонних треугольника, сложенных своими сторонами, дадут направления OM и OA, а колышки в A, O, M, N, C и D можно разместить с помощью прямых измерений. Дуга MEGN может быть вычерчена с помощью веревочной петли, и, наконец, основной круг также можно вычертить с помощью той же петли, привязанной к столбу B и перекинутой через колышек O.

Хотя приплюснутый круг типа А несколько более сложен для построения, колец типа А существует больше, чем колец типа Б. В их число входят кольцо Касл-Ригг близ Кезика в графстве Камберленд (фото VIII) и Стоячие Камни Торхауса близ Уигтауна в Шотландии. Самое большое каменное кольцо Бернмурской группы в графстве Камберленд также принадлежит к этому типу, и оно особенно интересно, потому что внутри него находятся пять маленьких кернов. Центры четырех кернов расположены по эллипсу с эксцентриситетом 0,72, а центр пятого лежит на одной из осей эллипса. Комбинации различных геометрических фигур в одном памятнике не так уж редки, но одна фигура внутри другой — это действительно редкость.

В основе яйцеобразных фигур лежат пифагоровы треугольники. Яйцеобразная фигура типа I (рис. 3.5) включает два треугольника с общим катетом. Периметр такой фигуры представляет собой комбинацию дуг трех радиусов: одна с центром в A радиуса AE, две с центрами в C и D радиусами CF и DE, а острый конец фигуры образован дугой круга с центром в B и радиусом BG. Построить эту фигуру удивительно просто.

а. Начертите на земле с помощью мерных реек или веревок два пифагоровых треугольника, как показано на рис. 3.5, а затем вбейте столбики в вершинах углов A, B, C и D.

б. Решив, какого размера должна быть фигура, сделайте веревочную петлю, закрепите ее на столбике в точке C, перекиньте через столбик в точке A и проведите назад в точку E. где маркировочный кол находится в начале вычерчивания фигуры.

в. Начертите тупой конец яйцеобразной фигуры, проведя кол по окружности к F, но, достигнув точки F, перенесите веревку через столбик и продолжайте чертить против часовой стрелки. Радиус круга автоматически изменится, как только петля сойдет со столбика в точке A.

г. Продолжайте чертить до точки G и на этот раз дайте веревке лечь на столбик B, так что кол вычертит острую часть яйцеобразной фигуры до H.

д. Теперь снимите петлю со столба C и накиньте ее на столб D, чтобы начертить остающуюся дугу HE.

Рис. 3.5. Геометрия яйцеобразной фигуры типа I

Существует много вариантов пропорций яйцеобразных фигур. Во-первых, для первоначального расположения четырех столбов можно использовать любой прямоугольный треугольник, а, кроме того, веревку можно взять либо относительно короткую, что даст очень заостренную фигуру, либо длинную, и тогда фигура выйдет закругленной. При построении каменных яйцеобразных фигур наиболее популярным был треугольник с отношением сторон 3:4:5 — примером этому служат Кернпеппл-Хилл в графстве Уэст-Лотиан и Клейва в графстве Инвернесс, где такую форму имеют каменные кольца, окружающие круглый коридорный могильник. Как и в случаях с эллипсами, имеются памятники, где использовались почти пифагоровы треугольники — например, в Бар-Хилле (графство Роксбро). Отношение сторон исходного треугольника составляет там 11:13:17 (11² + 13² = 290, 17² = 289), и различие между ним и истинным пифагоровым треугольником практически не поддавалось измерению...

Наиболее замечательной планировкой, опирающейся на этот тип яйцеобразной фигуры, обладает, по-видимому, Вудхендж (рис 3.6). Если истолкование, которое дает профессор Том, верно, то для его постройки был выбран треугольник с отношением сторон 12:35:37, который, как мы уже указывали выше, использовался в эллипсе Давиота. В Вудхендже не было каменных колец, и считается, что когда-то он представлял собой больше крытое деревянное строение. Его обнаружили в 1925 г. при помощи аэрофотосъемки, и дальнейшие раскопки выявили шесть концентрических колец лунок из-под столбов — каждая лунка теперь отмечена бетонным столбиком. Расположение этих лунок вполне может быть представлено шестью яйцевидными фигурами с общим исходным треугольником, причем каждая следующая вычерчивалась за счет удлинения веревочной петли перед началом разметки нового кольца. Самая внутренняя фигура, как и следовало ожидать, если она вычерчивалась таким способом, очень узка, а самая внешняя — почти круглая, с промежуточными формами между ними Не составляет никакою труда вычислить длину веревочных петель, использовавшихся для разметки Они равны (начиная от внутреннего кольца) 18,61, 21,24, 23,90, 26,54, 31,82 и 34,46 м Петля увеличивалась почти на одну и ту же длину — 2,64 м — каждый раз, когда строители переходили от одного кольца к другому, за исключением перехода от четвертого кольца к пятому, когда увеличение было вдвое больше. Вудхендж особенно интересен тем, что на его основе можно высказать некоторые предположения относительно причин выбора этих странных геометрических фигур, и мы к этому еще вернемся.

Рис. 3.6. План Вудхенджа. Цифры около колеи показывают их длину в мегалитических ярдах. Линии иллюстрируют построение яйцеобразной фигуры типа I с помощью треугольника со сторонами AB = 6 м. ярдов, AC = 17,5 м. ярда, BC = 18,5 м. ярда. По рисунку из книги А. Тома Megalithic Sites in Britain

Яйцеобразные фигуры типа II сходны с фигурами типа I в том, что они тоже строятся на основе пары прямоугольных треугольников, но в этом случае у треугольников общей является гипотенуза (рис. 3.7) При их построении, как и для фигур типа I, начинают с двух пифагоровых треугольников, в вершинах которых затем устанавливают столбы. Веревочная петля накидывается на столб в точке B, закрепляется на столбе C и к свободному ее концу привязывается маркировочный кол, которым и начинают чертить дугу от точки E. Дуга большого круга чертится от E до F, причем петля все время захлестнута вокруг столба C. Та же веревка используется для меньшей дуги: ее перекидывают через столб A и вокруг столба C, а затем через столб B сначала с одной его стороны, а потом с другой, чтобы начертить дугу GH. Две прямые линии фигуры, FG и EH, приходится размечать отдельно с помощью реек или туго натянутых веревок.

До сих пор удалось выявить очень мало фигур такого типа, но подобно всем остальным неправильным кругам они встречаются от одного конца Великобритании до другого. Например, яйцеобразная фигуре типа II имеется среди трех колец на Бодмин-Мур в Корнуолле, носящих название Вопленики и находящихся примерно в 6,5 км к северу от Лискарда. Оно имеет в основе треугольник с отношением сторон 3:4:5, так же как яйцеобразная фигура в Бакленд-Форде (Дартмур) примерно в 9 км к востоку от Бакстфастли.

Рис. 3.7. Геометрия яйцеобразной фигуры типа II

В Шотландии, в графстве Берик, неподалеку от городка Лодер есть малоприметное каменное кольцо Борроустон-Риг. Треугольник, на котором оно построено, не точно прямоугольный, так как длины его сторон равны 7,88, 10,17 и 12,87 м, т.е. их отношение составляет 3,06:3,95:5. Отступление от простого треугольника с отношением сторон 3:4:5 невелико, и уменьшение длины одного из катетов компенсируется увеличением другого, так что треугольник этот почти точно прямоугольный. Было ли такое изменение преднамеренным или нет, остается неясным, но выбор именно этих размеров с длиной петли 33,6 м добавляет еще одно усложнение: окружность малого круга проходит через центр большого. Создается впечатление, что строители, спланировавшие и воздвигшие каменное кольцо Борроустон-Риг, щеголяли своей технической виртуозностью и хвастали перед современниками, насколько они овладели новонайденными приемами (рис. 3.8).

И наконец, имеется несколько каменных колец, возможно всего четыре, отличающихся гораздо большей сложностью. Профессор Том назвал их составными кольцами, потому что хотя они и имеют в своей основе правильные окружности, но включают также дуги с несколькими разными радиусами. Два образчика этого типа находятся в Уэльсе в графстве Монтгомери — Моэл-Ти-Ухаф вблизи Уэлшпула (фото X) и Керри-Поул близ Ньютауна. Есть составное кольцо в Истер-Делфур близ Авимора в горной Шотландии. Как и приплюснутые круги и яйцеобразные фигуры, их можно вычертить на земле с помощью веревочных петель, проходящих вокруг правильно расположенных столбов и над ними. Описания их геометрических построений можно найти в книгах Тома.

Единственный пример составного кольца в Англии — это огромное каменное кольцо в Эйвбери. Оно необычно в нескольких отношениях: своими огромными размерами (диаметр 370 м), разнообразными каменными конструкциями внутри него (два каменных кольца по 103,6 м в диаметре каждое и другие фигуры из вертикальных камней) и тем, что в его очертаниях есть изломы. Профессор Том провел подробные съемки Эйвбери и истолковывает его геометрию как дуги семи окружностей с разными радиусами и разными центрами. Три центра лежат в вершинах треугольника с отношением сторон 3:4:5, и все семь геометрически взаимосвязаны. Его анализ кольца критиковал Фримен, который утверждает, что дуги других окружностей с другими радиусами точнее совпадают с положением камней, но при этом исчезает геометрическая связь центров. С археологической стороны тоже возникают трудности. Датировка Эйвбери пока еще окончательно не установлена, но это очень раннее кольцо, возможно, возведенное еще в XXVI в. до н.э. Трудно согласиться с тем, что столь изысканная геометрическая фигура была создана в эпоху, когда неправильные круги только-только начинали появляться. Некоторые археологи считают, что круги Эйвбери строились без предварительно разработанного плана и что сложное толкование порождено попыткой навязать порядок там, где его не было.

Рис. 3.8. План Борроустон-Рига. По рисунку из книги А. Тома; цифры внутри фигуры — его измерения расстояний в мегалитических ярдах

В начале главы мы упомянули, что не все археологи были готовы принять идею, будто мегалитические люди воздвигали неправильные каменные кольца, располагая их по заранее намеченным фигурам вроде приплюснутых кругов, яйцеобразных фигур и эллипсов, и здесь есть смысл рассмотреть имеющиеся данные. Прежде всего до настоящего времени были исследованы сотни памятников — главным образом профессором Томом, но не только им одним — и было обнаружено немало примеров всех указанных некруговых фигур. Нам известно, что наметить для кольца форму правильного круга даже с большой точностью было очень просто, а потому логично предположить, что видоизмененные круги также воздвигались сознательно. Мы не знаем наверное, как именно это делалось, но описанные выше методы использования столбов, веревочных петель и маркировочных кольев позволяют легко строить и более сложные фигуры. Вы можете сами убедиться в этом, попробовав где-нибудь на пляже или на футбольном поле. Необходимо только иметь возможность точно измерять длину отрезков и знать, что треугольники с определенным отношением сторон обязательно будут прямоугольными. Мы можем считать несомненным, что приемы правильных измерений длины были уже разработаны, иначе камни Стоунхенджа не удалось бы подогнать друг к другу — а это лишь наиболее эффектный пример из многих и многих. Знания теоремы Пифагора не требовалось — достаточно было методом проб и ошибок установить, что некоторые треугольники более удобны, чем другие. Короче говоря, для того чтобы вычерчивать все эти разнообразные фигуры, не надо особенно большого искусства или знаний — во всяком случае, они совершенно бледнеют в сравнении с инженерными способностями, которых требовало строительство мегалитических могильников или Силбери-Хилла. Имеющиеся в нашем распоряжении данные весомо свидетельствуют в пользу того, что строители мегалитических каменных кругов и колец сознательно использовали некруговые геометрические фигуры.

Тем не менее законно задать вопрос — а нельзя ли было создавать такие фигуры с помощью других приемов, возможно, более простых? Нельзя ли было вычерчивать приплюснутые круги и яйцеобразные фигуры, комбинируя полукруги и эллипсы? Для двух типов приплюснутых кругов вполне законно попробовать вычертить эллипс, наиболее напоминающий уплощенную часть кольца. Наметим на рис. 3.3 и 3.4 две точки (F₁ и F₂), расположенные на горизонтальном диаметре колец так, чтобы их расстояние от B равнялось радиусу главного круга, т. е., иначе говоря, чтобы BF₁ = BF2 = OA. Теперь F₁ и F₂ являются фокусами эллипса, который можно начертить с помощью веревочной петли, как было описано выше. Эксцентриситеты эллипсов можно вычислить по прямоугольному треугольнику BF₁O (они в обоих случаях составляют OF₁/OA) — эксцентриситет окажется равным 0,567 для кругов типа А и 0,693 для кругов типа Б. На рис. 3.9 эти эллипсы наложены на приплюснутые крути, построенные вышеуказанным способом, чтобы читатель получил наглядное представление о том, насколько они совпадают. Эллипс дает вполне приемлемое приближение к кольцу типа Б, но не соответствует кривизне типа А. Эллипсы с такими эксцентриситетами нигде больше не встречаются, и в целом представляется маловероятным, чтобы в раннем бронзовом веке для построения приплюснутых кругов использовались эти альтернативные варианты.

Не так легко сделать подобное сравнение для яйцеобразных фигур, потому что при их построении употребляется слишком много разных линейных размеров. Меняться могут не только формы лежащих в их основе треугольников, но и длина веревочной петли, и, в сущности, каждая такая фигура является уникальной. Мы приводим лишь одно сравнение: на план яйцеобразного кольца в Клейве наложена часть подогнанного к нему эллипса (эксцентриситет 0,574). Обе кривые практически совпадают (рис. 3.10).

Более подробные раскопки могут в будущем дать дополнительные сведения о том, как вычерчивались каменные кольца. При очень большой удаче исследователь может обнаружить следы от временных столбов, которые использовались на первых этапах строительства. Их расположение во многом прояснило бы вопрос, пользовались ли строители описанными способами построения или же совершенно иными.

Если мы готовы поверить, что строители сознательно придавали каменным кольцам формы особых геометрических фигур, то возникает неизбежный вопрос: «Зачем они это делали?» Чем не подходил им простой круг, почему они вынуждены были прибегать к более сложным расположениям камней, требовавшим больше хлопот? Во всяком случае не ради внешнего вида колец — стоя в центре приплюснутого круга или эллипса с малым эксцентриситетом, ни один человек не заметит отклонения. Профессор Том предлагает для эллипсов и яйцеобразных фигур следующее объяснение: строители каменных колец придумали собственную единицу длины и пытались по возможности строить круги и кольца с периметрами, равными целому числу таких единиц, умноженному на 2,5. И — словно одно это еще не было достаточно трудным — они одновременно пытались добиться того, чтобы диаметры этих фигур были равны целому числу таких единиц. Том назвал эту единицу «мегалитическим ярдом» (сокращенно м. ярд) и утверждает, что 1 м. ярд равен 0,829 м, из чего следует, что 2,5 м. ярда дают «мегалитический род», равный 2,073 м.

Рис. 3.9. Приплюснутые круги и наиболее близкие к ним эллипсы

С кругом такое построение не получается. Длина окружности равна произведению 2π на радиус. Греческая буква π обозначает число 3,1415926..., которое приблизительно равно 3⅐ и не может быть выражено точно ни простой, ни десятичной дробью. Такие числа называются иррациональными.

Тщательно выбирая диаметры, можно найти такую комбинацию диаметра и окружности, которая будет почти отвечать этим требованиям. Например, круг с диаметром в четыре любые единицы длины имеет окружность 12,566 этой единицы, что составляет 2,5×5,0265 единицы, а 5,0265 отличается от целого числа менее чем на 3% такой единицы. У круга с диаметром в 27 единиц длина окружности будет равна 2,5×33,93 единицы, а 33,93 отличается от 34 всего на 0,02%. Профессор Том проанализировал размеры очень многих каменных колец и пришел к выводу, что конкретные диаметры (в мегалитических ярдах), дающие эти и сходные комбинации, заметно предпочитались их строителями. Этот анализ является одним из основных источников, по которым он вывел длину мегалитического ярда. Мнение статистиков относительно реальности существования мегалитического ярда будет рассмотрено ниже, а пока примем идею профессора Тома и посмотрим, помогает ли она объяснить остальные фигуры.

Можно подумать, что приплюснутые круги — результат сознательных попыток создавать кольца с окружностью, близкой к утроенному диаметру, и таким образом избежать иррациональности π. Приплюснутый круг типа А имеет периметр, равный произведению радиуса круговой части на 2×3,0591, а для типа Б он равен произведению главного радиуса на 2×2,8746. Но 2,8746 отличается от 3,0 не меньше чем л, и множитель в приплюснутом круге типа А, хотя он и отличается от 3,0 менее чем на 2%, можно было бы еще более приблизить к этому числу, чуть-чуть изменив построение. Все это как будто не объясняет построения приплюснутых кругов.

Искали ли строители таких кругов комбинации диаметра и периметра, дающие целые числа, как они искали их для правильных кругов? По-видимому, нет. Иначе они, несомненно, проявляли бы особый интерес к приплюснутым кругам типа А с диаметром, скажем, 18 м. ярдов, который дает периметр 22,03 м. рода, и 27 м. ярдов, который дает периметр 33,04 м. рода. И точно так же у приплюснутых кругов типа Б преобладали бы диаметры в 20 м. ярдов и их производные, периметры которых являются производными от 22,997 м. рода. Но такие диаметры не обнаружены. Хотя Том и утверждает, будто замечается предпочтение диаметров, содержащих целое число мегалитических ярдов, нет никаких данных, указывающих на предпочтение периметров, кратных 2.5 м. ярда. Изучение геометрии этих фигур пока не подсказало никакого объяснения, почему были выбраны именно они.

Рис. 3.10. Геометрия кольца в Клейве. По рисунку А. Тома; цифры внутри фигуры — его измерения расстояний в мегалитических ярдах. Штриховая линия в нижней части фигуры — часть эллипса с фокусами в F₁ и F₂

Другое дело — эллипсы и яйцеобразные фигуры. Эллипс в зависимости от эксцентриситета может изменять форму в широких пределах между двумя крайними случаями: начиная от круга при эксцентриситете, равном нулю, до прямой линии при эксцентриситете, равном единице. Его периметр может колебаться от л, умноженного на длину его большой оси (в случае круга), до удвоенной длины его большой оси (в случае прямой линии). А потому, подбирая соответствующий эксцентриситет, вполне можно добиться того, чтобы большая ось эллипса и его периметр одновременно выражались целыми числами в любых избранных единицах. По мнению Тома, мегалитических архитекторов даже и это не удовлетворяло. Мы видели, что каждый эллипс содержит в себе прямоугольный треугольник (F₁OB на рис. 3.2) и что в каменных кольцах эти треугольники иногда бывали пифагоровыми. Трудная задача, которую, возможно, ставили перед собой строители, заключалась в том, чтобы все три стороны треугольника выражались целыми числами мегалитических ярдов. Разумеется, добиться этого в точности невозможно и даже приблизительно очень трудно. Довольно удачная попытка была сделана в Лоунхед-оф-Давиот близ Мелдрума в Шотландии, где каменный «круг» с поваленным камнем на самом деле представляет собой эллипс с эксцентриситетом 0,36. (Это не тот эллипс, который находится в Давиоте под Инвернессом.) В основе лоунхедского эллипса лежит почти пифагоров треугольник со сторонами 14, 5 и 13,08 м. ярда (очень близко к отношению сторон 14:5:13), а периметр эллипса составляет 42,54 м. ярда, т.е. 17,016 м. рода (очень близко к 17 м. родам).

Не всегда было возможно настолько приблизиться к целым числам. В общем строители либо клали в основу эллипса пифагоров треугольник и допускали, чтобы периметр не был точно кратным 2,5 м. ярда, либо они добивались того, чтобы длина периметра была равна произведению 2,5 на целое число мегалитических ярдов, и искажали треугольник. В последнем случае они оставляли без внимания длину малой оси эллипса и добивались того, чтобы и большая ось и расстояние между фокусами выражались целым числом мегалитических ярдов. При таких условиях длина веревки, использовавшейся для разметки эллипса, также содержала целое число ярдов. Так, периметр эллипса в Калленише, в основе которого лежит треугольник с отношением сторон 3:4:5, равен 14,18 м. ярда, т.е. 5,67 м. рода, а это недостаточно близко к 6, чтобы считать периметр хорошо подогнанным. С другой стороны, в Сандс-оф-Форви, на побережье примерно в 20 км севернее Абердина, эллипс имеет в основе треугольник со сторонами 16,5, 6 и 15,37 м. ярда и его периметр очень точно укладывается в производное от 2,5 м. ярда, поскольку он равен 20,03 м. рода.

Периметры яйцеобразных фигур обладают теми же свойствами, что и периметры эллипсов. Яйцеобразная фигура в Клейве опиралась на треугольник со сторонами 6, 8 и 10 м. ярдов. Радиус полуокружности равен 19 м. ярдам, и следовательно, фигура вычерчивалась петлей длиной 25 м. ярдов. Периметр ее, согласно вычислениям, равен 125,36 м. ярда, т.е. 50,14 м. рода. Если такое истолкование его построения верно, то эта яйцеобразная фигура может считаться весьма удачной попыткой добиться того, чтобы и периметр, и стороны треугольника, а следовательно, и длина, и ширина самой фигуры все выражались целым числом.

Однако наиболее тонкие особенности, заложенные в яйцеобразных фигурах, мы находим, рассматривая множественные кольца лунок из-под столбов в Вудхендже. Длина петли, использовавшейся для разметки этой системы, увеличивается на одну и ту же величину от кольца к кольцу. А это означает, что и длина периметров от кольца к кольцу увеличивается на одну и ту же величину. Согласно данным съемок Тома, периметры колец соответственно равны 32,9, 51,2, 66,7, 87,0, 115,4 и 134,4 м. Значение этих чисел станет более ясным, если мы соотнесем длину периметров всех шести колец с длиной третьего кольца, считая от центра. Мы получим отношение 0,49:0,77:1,00:1,30:1,73:2,01, т.е. образуется ряд ½, ¾, 1, 1¼, 1¾ и 2 с ошибкой не более нескольких процентов. Как только выбран исходный треугольник, периметр, длина и максимальная ширина колец зависят только от длины веревочной петли, и можно предположить, что веревка для каждого кольца подбиралась так, чтобы длина и ширина колец увеличивались каждый раз на одну и ту же постоянную величину — что и имеет место в действительности. Но ни в одном из этих рядов размеров мы не находим столь точных отношений, как у периметров, а потому вполне логично заключить, что главной целью при планировании Вудхенджа было увеличение периметров по мере удаления от центра на равные доли. Вудхендж дает много материала в поддержку гипотезы Тома, что самым важным элементом колец для мегалитических строителей были периметры.

К этому же заключению можно прийти, и не вводя понятия мегалитического ярда, но если принять его длину, предлагаемую Томом, т.е. 0,829 м, то периметры равны 39,7, 61,8, 80,5, 104,9, 139,2 и 162,1 м. ярда, что, по мнению Тома, явилось следствием попытки сделать их равными 40, 60, 80, 100 и 160 м. ярдам.

Эти результаты многими были встречены очень скептически. Хотя общие очертания колец из лунок, оставшихся от столбов, очень хорошо укладываются в яйцеобразные фигуры, некоторые лунки на снятых Томом планах находятся в двух и более метрах от намеченных им линий. Если геометрическое построение Вудхенджа было так важно для его строителей, то мы могли бы ожидать большей точности и в установке столбов. Однако Том делал съемку по бетонным столбикам, которые, возможно, не всегда попадали точно в первоначальные лунки. Существуют некоторые различия между планом, который сняли во время раскопок супруги Каннингтон, и планом Тома, и мы не знаем, насколько точны были первые съемки. Далее, третье снаружи кольцо слишком велико и поэтому выпадает из последовательности. Том объясняет эту аномалию следующим образом: это кольцо — с самыми большими лунками, и следовательно, с самыми толстыми столбами, но если брать размеры не по центру лунок, а по их внутреннему краю, кольцо вполне укладывается в схему.

В расположении столбов Вудхенджа есть и другие интересные особенности. Как и у Стоунхенджа, его ось ориентирована на точку восхода Солнца в день летнего солнцестояния, а узкие концы яйцеобразных фигур обращены на северо-восток. Число столбов в кольцах — 12, 18, 18, 16, 32 и 60 — было выбрано так, чтобы по обеим сторонам оси их оказалось равное число. И наконец, Каннингтоны нашли на его оси могилу ребенка в месте, которое, по-видимому, находилось неподалеку от одного из углов лежащего в основе фигуры треугольника.

Ни одна из геометрических особенностей Вудхенджа не исключает возможности того, что он служил основанием большого крытого строения. Более того, большие лунки третьего кольца имеют скаты, показывающие, что в них были установлены внушительные бревна. Однако в плане других памятников, где сохранились следы деревянных строений: Мардена, Маунт-Плезанта, Даррингтонских Стен и Святилища, — все вышеуказанные сложности отсутствуют. Они размечались как простые круги, хотя аккуратно и тщательно, о чем свидетельствует симметричный план Маунт-Плезанта, где в каждом квадранте строения располагалось равное число столбов.

Одна из причин сложности Вудхенджа по сравнению с другими деревянными строениями, возможно, заключается в его особой ритуальной важности. Считается, что он был построен относительно поздно — около 2250 г. до н. э., тогда как другие сходные памятники датируются XXVI в. до н.э. Дата постройки Вудхенджа показывает, на каком этапе усовершенствовалась геометрия яйцеобразных фигур, и это особенно ценно потому, что каменные кольца дают лишь крайне скудный материал для их датировки. Пока еще невозможно предложить твердую хронологию для различных типов каменных колец или связать их с другими характерными особенностями культуры. Все немногочисленные имеющиеся об этом данные были собраны Обри Берлом, который вывел из них несколько предварительных заключений.

Независимо от периода постройки большинство каменных колец имело форму правильного круга. Примерное соотношение разных типов фигур следующее: ⅔ составляют правильные круги, ⅙ — приплюснутые круги, ⅑ — эллипсы и 1/18 — яйцевидные фигуры. Наиболее ранние кольца были правильными кругами, как и следовало ожидать, поскольку такие круги легче всего размечать. Некоторые приплюснутые круги могли быть построены в позднем неолите, но другие новшества — эллипсы и яйцеобразные фигуры — относятся к раннему бронзовому веку, причем большинство появилось после 2000 г. до н. э. С развитием более сложных фигур происходило общее уменьшение размеров каменных колец, и доля больших колец в раннем бронзовом веке заметно меньше, чем в позднем неолите.

Мегалитическая геометрия не всегда проявлялась в таких крупных масштабах. Том изучал чашевидные и кольцевые метки с тем же прилежанием, что и каменные круги и кольца. Подавляющее большинство среди них составляют простые круги и углубления, но есть и некоторое количество интересных фигур, в том числе спирали, эллипсы и яйцеобразные. В резьбе по камню выявляются те же особенности, что и в каменных памятниках, — яйцеобразные фигуры и эллипсы опираются на пифагоровы треугольники. Четыре кольца, составляющие узор в Кардонесс-Хаусе близ Керккудбрайта в Шотландии, имеют яйцеобразную форму (тип I), и в основе их лежит вездесущий треугольник с отношением сторон 3:4:5 — его стороны соответственно равны 1,55, 2,07 и 2,59 см. Радиусы полукругов равны 3,11, 4,66, 7,24 и 9,57 см, что дает для периметров 20,7, 31,05, 46,6 и 62,1 см. Сходство между ними и Вудхенджем очевидно. Том вывел из этого заключение, что основой рисунка была малая единица измерения — мегалитический дюйм (м. дюйм), равный сороковой части мегалитического ярда, т. е, 2,07 см. В этих единицах периметры выражаются следующими цифрами: 10, 15, 22,5 и 30 м. дюймов.

Есть и другие примеры, которые нет нужды описывать здесь, поскольку они весьма сходны с геометрией каменных колец. Камни очень тверды, а потому использование для их разметки веревок, как это предполагается для больших сооружений, маловероятно. Том полагает, что употреблялись циркули в форме кремневых или кварцевых острий, вделанных в палки. Для каждого круга требовался бы свой циркуль, но поскольку диаметры выцарапанных кругов, как полагает Том, всегда были кратны мегалитическому дюйму, можно было бы обойтись небольшим количеством инструментов. Возможно, кольцевые метки делались не просто для интеллектуального развлечения, но и для опробования новых фигур, и для наставления учеников в искусстве и практике мегалитической геометрии.

Мегалитический ярд — одно из наиболее оспариваемых предположений профессора Тома. По его мнению, это была очень точная единица измерения, равная 0,829 м, которая применялась по всей северо-западной Европе при сооружении каменных кругов, колец и рядов. Он находит одинаковую длину мегалитического ярда с точностью до полусантиметра в Карнаке (Бретань), в Эйвбери (Англия) и в Бродгаре на Мейнленде (Оркнейские острова). В Стоунхендже он находит ту же длину мегалитического ярда в кольце лунок Обри и в сарсеновом кольце, хотя их разделяют две тысячи лет. Если Том прав, значит, эта чрезвычайно точная мера длины использовалась разными племенами в очень обширной области на протяжении чрезвычайно долгого времени. Следствия такого вывода для наших представлений о позднем неолите и раннем бронзовом веке были бы поистине колоссальны.

Из сходства керамики и из распределения топоров мы узнаем, что в этот период между различными племенами северной Европы существовали какие-то контакты, а широкое распространение различных типов каменных колец подтверждает, что контакты эти были, пожалуй, более тесными, чем простая торговля. Однако принятие единого эталона длины подразумевало бы чрезвычайно тесные культурные связи, существование которых не подтверждается археологическими исследованиями. Например, предлагаемые Томом очень точные единицы могли бы распространиться по всей области, только если бы в каком-то центре изготовлялись физические воплощения этих единиц (например, деревянные рейки), которые затем доставлялись бы разным группам, занятым возведением каменных колец. Их надо было при этом каким-то образом принудить к использованию привозных реек или убедить, что это им выгодно. Эталоны приходилось бы время от времени обновлять, потому что они изнашиваются и ломаются от долгого употребления, а это подразумевает непрерывность целей и традиций, не нарушенную даже появлением бикеров и последовавшими за этим культурными изменениями. Естественно, археологи отказываются поверить в существование мегалитического ярда, пока оно не будет подтверждено вескими и прямыми свидетельствами.

Нам совершенно не приходится рассчитывать на счастливую находку камня с метками и с надписью, объясняющей, что расстояние между этими метками есть мегалитический ярд, а потому мы должны обращаться к кругам и кольцам, проверяя, нельзя ли вывести из их современных соотношений какую-то единицу длины, которая, возможно, использовалась при их сооружении. Для этого применяются статистические методы. Они должны дать возможность обработать имеющиеся у нас неполные сведения, поскольку многие камни были передвинуты с их первоначального места, а съемки кругов не всегда велись с достаточной точностью.

Первые работы, в которых проводились поиски общей единицы — или модуля, как ее обычно называют в таком контексте, — принадлежат С.Р. Бродбенту, чьи основные исследования были связаны с биологическими науками. Он указал, что существуют две совершенно разные ситуации, требующие различных математических методов. Первая — это те случаи, когда мы считаем (или знаем из других источников), что какой-то модуль существовал, и имеем некоторое представление о его величине. Бродбент разработал статистический метод проверки списка диаметров каменных кругов, составленного Томом, чтобы выяснить, присутствует ли в них предполагаемая для модуля величина или нет. Вторая ситуация — это те гораздо более трудные случаи, когда нет никакого предварительного представления о существовании или величине модуля и список диаметров надо обработать статистически, чтобы проверить, присутствует ли в них хоть какой-нибудь модуль. Эти два подхода в применении к данным о каменных кругах дают довольно различные результаты: первый подтверждает идею существования мегалитического ярда гораздо более убедительно, чем второй. Некоторые специалисты по статистике считают, что первый метод вводит в заблуждение, и поэтому в табл. 3.1 приведены только результаты, полученные вторым методом.

Несколько иной подход к решению этого вопроса был разработан профессором Кендоллом, который сделал сообщение о нем на конференции «Место астрономии в древнем мире» в 1974 г. Его лекция, предназначенная для неспециалистов, содержала объяснение статистических проблем, возникающих при поисках модулей, и читателям, которые хотели бы ознакомиться с этим вопросом глубже, мы рекомендуем обратиться к ней.

Цифры в табл. 3.1 основаны на результатах (только для каменных колец), полученных Бродбентом и Кендоллом. Рядом с каждой найденной для модуля длиной указывается статистическая значимость результата. Попросту говоря, если значимость равна 0,01, то есть только один шанс на сто, что результаты не объясняются случайностью. Бродбент и Кендолл пришли к сходным выводам. Оба они нашли в размерах шотландских каменных кругов модуль, близкий к 1,66 м, который мы можем истолковать, как 2 м. ярда. Английские и уэльские каменные круги не дали четких результатов — анализ с довольно малой степенью значимости выявил несколько разных модулей. При объединении результатов для всей страны шотландские данные перевешивают все остальные, и анализ вновь выявляет модуль в 2 м. ярда. Кендолл пришел к заключению, что эти результаты, хотя они и не полностью подтверждают гипотезу Тома, все-таки достаточно обнадеживают, чтобы имело смысл провести более точную съемку памятников и собрать данные о других каменных кольцах. Собственно говоря, еще нет достаточного количества измерений, чтобы прийти к окончательным выводам, особенно потому, что данные распадаются на группы, относящиеся к разным частям страны.

Таблица 3.1

Совсем недавно Фримен провел собственное исследование приводимых Томом размеров каменных колец с помощью еще одного метода. Результаты, полученные им для шотландских колец, хорошо согласуются с результатами Кендолла, и он считает, что имеются доказательства использования мегалитического ярда в Шотландии, однако для каменных кругов Англии и Уэльса он не нашел указаний на то, что там употреблялась какая-то универсальная единица. Он применил свой метод проверки к интервалам между камнями в рядах Карнака, рассматривая расстояния, найденные при съемках самим Томом, и пришел к выводу, что нет никаких признаков последовательного использования при размещении этих камней определенной единицы длины и что нет никаких данных в пользу утверждения Тома, будто в основе их геометрических построений лежал мегалитический род.

Хотя споры и дискуссии, несомненно, будут продолжаться, выводы последнего времени отвечают здравому смыслу. Несомненно, для разметки геометрических фигур необходимо было проводить измерения, и более сложные памятники, вроде Вудхенджа, невозможно было бы создать, если бы измерения эти не были точными. Но почему единица длины, использовавшаяся при строительстве одного памятника, обязательно должна была совпадать с теми, которые использовались в других, уже далеко не столь очевидно, и чем дальше отстоят друг от друга эти памятники в пространстве и во времени, тем менее правдоподобным выглядит такое предположение. Однако в Шотландии как будто действительно была принята общая единица длины — возможно, только одной культурной группой и в течение ограниченного периода.

Статистический анализ ничего не говорит нам об использовании лишь приблизительно равных единиц. Мы легко можем вообразить группу людей раннего бронзового века, решивших воздвигнуть каменное кольцо вроде того, которое, как они слышали, имелось в другом селении. Если они хотели отступить от простого круга, им скорее всего нужно было заручиться помощью специалиста из того места, где существовали традиционные правила установки камней. Такой специалист, конечно, знал, какая точность требуется в работе, но вместо того, чтобы принести с собой эталон, он изготовил бы его на месте, использовав размеры тех или иных частей человеческого тела. Для своей линейки длиной 2 м. ярда он мог взять рост мужчины, или средний рост нескольких мужчин, или же размах вытянутых рук. Или же для своего варианта мегалитического ярда он мог взять средний шаг. Любой из этих способов обеспечил бы его практичным измерительным инструментом без всякой необходимости прибегать к сложным научным методам.

Хотя нам трудно принять гипотезу о широком распространении стандартного мегалитического ярда, не следует впадать в другую крайность и отрицать или принижать достижения в геометрии и измерениях, достигнутые людьми в течение позднего неолита и раннего бронзового века. Взаимосвязь между тремя единицами длины — 1 м. род = 2,5 м. ярда = 100 м. дюймам — дает очень практичную и логичную систему единиц. Если они хотя бы в отдельных местностях были действительно такими точными и четко определенными, как утверждает профессор Том, значит, бикеры располагали таким набором линейных мер, какого не знала ни одна эпоха до изобретения метрической системы после французской революции 1789 г.

Примечания

*. Под пифагоровыми треугольниками здесь и далее подразумеваются прямоугольные треугольники, отношение сторон которых выражается целыми числами. — Прим. ред.