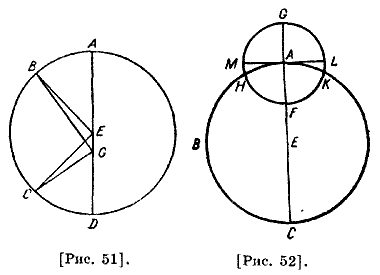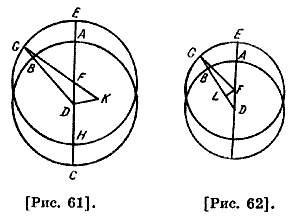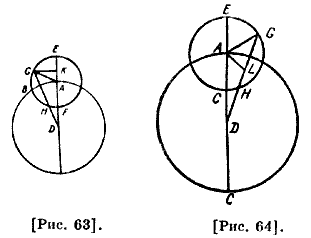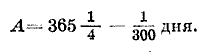Аль-Фараби

КОММЕНТАРИИ К "АЛЬМАГЕСТУ" ПТОЛЕМЕЯ

* О временной величине года * О гипотезах, предполагаемых для равномерного движения, происходящего по кругу * О видимом неравенстве движения Солнца * Об определении частных [значений] неравенств * О неравенствах суток * Примечания *

ТРЕТЬЯ КНИГА⁹⁵

О временной величине года⁹⁶

Среднее движение — это такое действительное или предполагаемое движение, при котором [светило] за равное время [проходит] одинаковые [дуги]. Это движение светила по предположению происходит в соответствующей ему небесной сфере, охватывающей Землю. Оно характерно или самому светилу, или сферическому телу, несущему светило и передвигающему его вдоль эклиптики благодаря своему движению. За равное время оно проходит равные дуги, а центральные углы при центре, [стягиваемые] этими дугами, равны. Это движение называется равномерным⁹⁷.

Если бы светила или несущие их [тела] обладали одинаковыми движениями за равное время по отношению к эклиптике и проходили бы равные дуги на ней за одно и то же время, то среднее равномерное движение было бы достаточным для [установления] эфемерид⁹⁸. Если измерить [дуги] эклиптики, то нельзя обнаружить, что при движении планет они за равное время проходят равные дуги, на самом деле они различны: иногда меньше, иногда больше. Среднее [движение — промежуточное] между наименьшим и наибольшим. Поэтому оно и называется средним. Аномалия встречается во многих вещах, которые упомянем [ниже].

Каждая планета имеет свою сферу, в которой ее равномерное движение описывает за равные времена равные дуги, действительные или предполагаемые.

Истинное движение — это такое движение, которое [фактически] находится но отношению к эклиптике. В движениях планет может быть более одной аномалии, но у Солнца имеется только одна аномалия, которую мы и упомянем [ниже].

35 Известный способ нахождения среднего [движения] таков: требуется найти промежуток времени, за который планета всегда возвращается к одному и тому нее положению, то есть к одной и той же точке или к разным точкам, прошедшим равные дуги сверх полных кругов, безразлично в одном обороте или в следующих друг за другом оборотах. Последовательные возвращения планеты могут быть различными, но эта аномалия имеет предел. Затем движение возвращается к своему началу и начинается в том месте, где еще не было аномалии, и аномалии повторяются в тех же положениях и последовательности до последней из них. Поэтому место одного возвращения определяется многими возвращениями, все вместе они являются возвращением аномалии. Если имеется такой [промежуток] времени, за который планета всегда возвращается к одной и той же точке или к точкам, между которыми имеются равные дуги, или же аномалии всегда возвращаются, как мы упомянули, то этот промежуток времени переводится в сутки или часы. Затем одно полное и разделенное на равные дуги возвращение, в том числе и возвращение подобных аномалий, разделятся на этот [промежуток времени]. Полученное в частном является долей этого дня или часа. Затем по ней находится доля месяца, года и [периодов из нескольких] лет для среднего движения. Поскольку молено определить среднее | движение | этим методом, мы не отказываемся от него и не [стремимся] к его определению другими методами. Первое, что требуется для определения среднего движения, — это возвращение к одной и той же неподвижной точке или к точкам, между которыми имеются равные дуги. Если найдены возвращения такого рода, то есть за равные промежутки времени, то для определения среднего движения ограничимся этим. В противном случае потребуем другой род, затем третий, как будет показано в надлежащем месте.

Рассмотрение положения Солнца предшествует рассмотрению всех планет, так как определение их обстоятельств возможно только после определения движения и положения Солнца, как мы покажем⁹⁹ [ниже].

Птолемей начинает с уточнения среднего движения Солнца. Исследуя наблюдение за ним, он нашел, что различие в возвращении Солнца к одной и той же неподвижной точке эклиптики, по которой вычисляются эфемериды, несущественно. Когда эти [возвращения] оказывались различными, он находил, что причиной этого была неправильность или в делениях, или в их установке, или же упущение исследователя при пользовании этими [инструментами] и наблюдение в неправильном направлении. Истинное наблюдение Солнца состоит в рассмотрении промежутка времени возвращения [Солнца] к одной и той же неподвижной точке эклиптики; предпочитаются точки равноденствий и солнцестояний, особенно, если [тело], несущее светило, не имеет другого движения по причине движения его апогея. Мы смотрим, являются ли эти промежутки времени равными. Если они равны, то среднее движение определяется было сказано. Наблюдая за Солнцем, Птолемей нашел эти промежутки времени равными и определил [величины] этих промежутков времени, которые мы упомянем ниже. Это наблюдение производилось с помощью кольца¹⁰⁰, сделанного из меди или другого металла и ограниченного четырьмя плоскими гранями, каждая противоположная пара из которых параллельна; его прочно устанавливали на неподвижной основе в плоскости небесного экватора, то есть посередине между солнцестояниями, как мы об этом уже сказали, что определено наблюдением; или же в плоскости круга, параллельного небесному экватору и проходящему через одну из точек солнцестояний; или же на каком-нибудь желательном для наблюдателя круге из параллельных кругов, описанных точками, отмеченными на эклиптике.

Установка в плоскости [круга] означает 36 описание круга в плоскости данного круга так, чтобы, продолжая диаметр этого внутреннего круга в обе стороны, можно было бы получить диаметр или хорду другого. Далее известно, что если кольцо такого рода установлено именно так на плоскости небесного экватора или в плоскости одного из параллельных кругов, проходящих через точки солнцестояния или через другие [точки] эклиптики, и если Солнце находится в точке равноденствия или в точке солнцестояния [или в другой точке эклиптики], то тень со стороны, примыкающей к Солнцу, полностью совпадает с противоположной стороной и никогда не упадет на грани, находящиеся с южной и с северной стороны, и [Солнце] полностью осветит эти две грани. В таком случае мы узнаем, что Солнце достигло этой точки.

Точно так же на кольце [можно] установить алидаду с двумя диоптрами¹⁰¹, чтобы алидада была симметричной и вращалась бы вместе с Солнцем. Это наблюдение трудно провести, если совпадение центра светила с рассматриваемой точкой происходит ночью. Поэтому [в таком случае] необходимо прибегнуть к другому наблюдению, которое мы упомянули в главе, посвященной определению склонения.

Известно, что если разделить пополам [расстояние] между пределом высоты, когда Солнце достигает предела склонения, и пределом понижения, когда Солнце достигает предела южного склонения, получится место, до которого поднимается Солнце, когда оно в точности находится на небесном экваторе. Если это происходит ночью, то мы рассмотрим разность между высотами предыдущего и последующего полудня [и разность между высотой последующего полудня] и высотой, соответствующей небесному экватору, тогда [вторая] разность относится к первой приблизительно так же, как [промежутки] времени с того момента, когда Солнце находится в данной точке [до последующего полудня] к [промежутку] времени между двумя полуднями.

Наблюдение с помощью солнцестояния трудно в обоих случаях, так как предел высоты и предел понижения отличаются в течение короткого [промежутка] времени и при этом различие незаметно, поскольку разность склонений по обе стороны от солнцестояния мала.

Рассматривалось возвращение Солнца к четырем точкам, при этом найдено, что эти возвращения [происходят] в равные [промежутки] времени. Точно такими же нашел их Гиппарх, за исключением осенних возвращений, когда наблюдается различие в четверть суток.

Птолемей обосновал причину этого в одном из упомянутых обстоятельств погрешностью в делениях инструмента или его [неправильной] установкой, так что если допускается погрешность в шесть минут, то есть в одну десятую градуса, то это [приведет] к указанному различию. Поэтому [погрешность] в одну минуту, принятая им в книге, может привести к отклонению от истины на половину дня, так как если Солнце отходит от точки равноденствия на четверть градуса, то это приведет к такой же [погрешности], как и шесть минут. Он упоминает, что, возможно, [люди] вначале установили инструменты точно, а затем оставили их, и эта [точность] нарушилась, а они не исправляли эти [инструменты] перед каждым наблюдением. Он упоминает также, что на кольце, установленном в Александрии, имелось неравенство между ее освещенной

и затемненной [частями] в день равноденствия. Эти [отклонения] отмечались в двух случаях — некоторые в одно время, а другие — в другое время, в одно и то же время они не наблюдаются. 37 Однако Птолемей отметил, что его многочисленные наблюдения и изученные им работы Гиппарха, которых еще больше, согласуются в том, что промежуток времени возвращения — один и тот же, и он равен тремстам шестидесяти пяти суткам и приблизительно четверти суток. О нем мы еще упомянем, его нельзя обнаружить на близких расстояниях, а можно определить только при более далеких наблюдениях, в которых накапливается значительная разница. При древних наблюдениях эта разница была подобна неравенству, [происходящему по причине неточной] установки инструментов и неизбежной ошибке. При этом он приблизительно указал величину этого недостатка, рассмотрев наблюдения Гиппарха и сопоставив их со своими. Он опирался на Гиппарха больше, чем на кого-либо другого. Наблюдения в [день] равноденствия — наиболее точные; те же, которые [производятся] в [дни] солнцестояний, трудно проверить. Птолемей приблизительно за триста лет до него установил, что если возвращение

[совершается] за триста шестьдесят пять с четвертью суток, имеется недостаток по величине одних суток. Поэтому для каждого года разница составляет одну трехсотую одних суток и, следовательно, [промежуток] времени возвращения — триста шестьдесят пять суток четырнадцать минут и сорок восемь секунд¹⁰². Затем он вычислил это по наблюдениям древних [астрономов] — Метона¹⁰³ и Евктемона¹⁰⁴, а затем Аристарха¹⁰⁵ и нашел, что получается то же самое и что Гиппарх согласен с этим во многих своих сочинениях.

Таков путь вычисления среднего прохождения [Солнца] по отношению к четырем точкам. Что касается возвращений Солнца по отношению к неподвижным звездам, то их можно найти двумя способами: путем наблюдения Солнца при восходе и заходе, если при этом видна одна из ярких неподвижных звезд, а также нахождением расстояния между Солнцем и этой звездой с помощью инструмента, который мы упомянем позже; путем наблюдения Луны в середине ее затмения, то есть, когда она диаметрально противоположна истинному Солнцу. [Затем] определяется ее положение на эклиптике в результате ее движения. Если при этом она не имеет параллакса, то легко установить ее градус путем определения высоты ее азимута и широты местности. Отсюда находится ее истинное положение на эклиптике с помощью принципов, приводящих [к этому] в случае, когда в середине затмения центр Луны не имеет широты. Отсюда можно определить градус Солнца, поскольку оно не имеет параллакса. Если же центр Луны имеет широту, то путь к этому более длинный и при этом легче ошибиться. Таким образом, промежуток времени возвращения [Солнца] оказывается больше упомянутого. Вот почему Гиппарх догадывался, что неподвижные звезды движутся около полюса эклиптики. Поэтому Птолемей пренебрег наблюдениями, проведенными относительно этих звезд. Нет разницы, считать ли солнечный год по возвращениям к неподвижным звездам, движущимся около точки, где Солнце и Луна [начинают] расходиться, или считать его по отношению к планете Сатурн; в обоих случаях годы получаются различными. Хотя это неравенство мало для близких оборотов, оно увеличивается для более далеких оборотов. Иногда это неравенство невозможно обнаружить. Наиболее грубыми являются наблюдения при затмениях, в которых требуется найти [положение] центра Луны относительно неподвижных звезд, когда Солнце на самом деле находится в диаметрально противоположной ей точке.

Далее Птолемей рассмотрел различные наблюдения, чтобы при их помощи найти возвращения Солнца и определить, совершаются ли они за равные промежутки времени, а с их помощью проверить [результаты], полученные другими методами. Гиппарх упомянул, что когда он провел вычисления для двух наблюдений лунного затмения, он при одном из этих наблюдений затмения расстояния Луны и Симака Безоружного¹⁰⁶ обнаружил, что положение Симака опережало точку осеннего [равноденствия] на шесть с половиной градусов, а через одиннадцать лет с немногим, когда провел вычисления для второго наблюдения, Симак Безоружный опережал точку 38 осеннего [равноденствия] на пять с четвертью градусов; к этому приводят измерения. Однако нельзя сказать, что Симак Безоружный за этот промежуток времени переместился на такую величину; поэтому он пришел к выводу, но без уверенного утверждения, что, возможно, у Солнца имеется еще одно неравенство, отличное от того, о котором мы будем говорить. Оно получается вследствие того, что его возвращения за равные промежутки времени не одинаковы.

Птолемей же отказался от этого метода, так как его наблюдения возвращений Солнца за тот же самый промежуток времени соответствовали указанным измерениям. Разница, полученная при наблюдении, когда для уточнения положения Луны было необходимо уточнить положение Солнца, не должна была вызывать сомнения в самом принципе, а происходит от второстепенных вопросов, поэтому в случае необходимости приходится сомневаться [только] в этих второстепенных вопросах. Кроме того, Луна может иметь параллакс, а инструменты, с помощью которых наблюдаются расстояния, могут обладать погрешностью. Возможно, причиной этого явилось то, что одно из этих двух наблюдений проводилось в исследованных обстоятельствах, а другое — в неисследованных, или же то, что исследование движения Солнца от точки весеннего [равноденствия] до середины времени затмения в его среднем продвижении не проводилось. Сам Гиппарх тоже знал это и поэтому не придавал своему [предположению большого] значения, он не утверждал, что Солнце обладает еще одним неравенством и не отвергал утверждения о том, что солнечный год является упомянутым промежутком времени. Поэтому неравенства, полученные при других наблюдениях, в которых имеется погрешность, не рассматривались. [Птолемей] указывал, что его цель состояла в рассмотрении всех встречающихся ему вещей до одной. Точно так же, когда Гиппарх наблюдал другие затмения, предварительно определяя истинное положение Солнца в середине затмения и рассматривая середины этих затмений относительно противоположного им центра Солнца; с их помощью он нашел положения неподвижных звезд, расстояния которых от Луны известны, а также доказал, что возвращения Солнца не отличаются существенно от тех, которые получаются при других наблюдениях. [Птолемей] сказал: когда я проверил [наблюдения при] затмениях с целью выяснения [этого вопроса], я обнаружил, что они не отличаются существенно от того, что должно быть. Я говорю, что нужно рассмотреть также состояние Солнца [и установить], имеет ли оно параллакс, с помощью наблюдений в весьма отдаленных друг от друга городах на севере и на юге, больше ли разница в его высоте в меридиане, которая вызвана различием широт [этих городов], а также наблюдать его там, где оно находится в зените и городах, недалеких от этих положений, и выяснить соответствует ли эта разница по высоте [разнице] широт. Если же окажется, что Солнце обладает параллаксом, то определяется его величина в соответствии с этим. Выясняется, что истинные высоты и тени предметов отличаются от наблюдаемых и вычисленных. Подтверждение существования параллакса [Солнца] приносит вред при уточнении места Солнца и времени, в которое оно приходит в данную точку; однако оно безвредно при определении солнечного года и промежутка времени возвращения Солнца к известной точке, так как, если возвращение по видимости таково же, как раньше, и город [один и тот же], возвращение по градусам эклиптики произойдет к одной и той же точке, однако отличной от той, которая определяется наблюдением.

39 Возвращение Солнца происходит на эклиптике в одной и той же точке, которая [может] быть отлична от той точки, которую дает наблюдение. Вообще если оно не возвратится в одну и ту же точку, то оно не возвратится и к одному и тому же параллаксу на высоте [точек] солнцестояний и равноденствий.

После того, как среднее движение [Солнца] получено этим способом, он захотел составить таблицы¹⁰⁷, избавляющие от вычисления каждого промежутка времени. Он поместил в них то, что пройдено Солнцем за один час, за 24 часа, за месяц, за год, за восемнадцать лет и за [промежутки времени], кратные восемнадцати годам. Если требуется найти то, что пройдено в среднем за данный промежуток времени, то найдем в таблице эти годы, сложенные или отдельные, и другие промежутки времени. Если в таблице имеется [промежуток], то возьмем градусы, минуты, секунды и все остальное, находящееся против этого. Если же имеется избыток, то посмотрим, какова его величина, и найдем в таблице то, что находится против него, и, прибавив к найденному, получим точное [среднее положение Солнца] в данный промежуток времени.

О гипотезах, предполагаемых для равномерного движения, происходящего по кругу

Если уже мы получили среднее движение Солнца, то для нахождения эфемерид Солнца этого недостаточно, так как за равные промежутки времени Солнце проходит неодинаковые дуги эклиптики. Оно проходит то меньше, то больше, как мы упомянем [ниже]. Наблюдением было найдено, что промежуток времени, за который оно проходит от весеннего равноденствия до летнего солнцестояния, отличается от того, за который оно проходит от последнего до осеннего равноденствия. Также было найдено, что [время], за которое оно проходит от осеннего до весеннего равноденствия, меньше времени, за которое оно проходит от весеннего до осеннего равноденствия. То же самое относится к частичным дугам. Но мы не можем сказать, что оно движется то медленнее, то быстрее, так как по закону небесных движений они равномерны и не имеют различий по отношению к самим себе. Если же они представляются и кажутся [неравномерными], то это [только] по отношению к нам¹⁰⁸.

Эта неравномерность происходит только по одной из двух причин. Первая причина: если Солнце движется по эксцентричному кругу, то та часть [круга], которая находится со стороны одной половины эклиптики, например северной, больше другой его части, если наибольшее удаление — с северной стороны. Солнце или любая планета движется или по своему [эксцентричному] кругу в своей сфере, тогда [оно проходит] больше его половины, или же по [самой] эклиптике, тогда [оно проходит] ее половину, а с другой [южной] стороны будет наоборот. Таким образом, оно пройдет обе половины эклиптики за разные [промежутки] времени¹⁰⁹.

Вторая причина: если [Солнце] движется не по кругу, концентричному с эклиптикой, и не по эксцентричному кругу, то его тело находится на круге, не охватывающем Землю, а не на кругах светил, охватывающих Землю. Оно движется по этому кругу, называемому эпициклом. Центр этого круга может двигаться по кругу, концентричному с эклиптикой¹¹⁰.

Далее ясно, что если движение планеты совершается по эпициклу в том же направлении, что и центр эпицикла, то нам кажется, что Солнце движется быстрее среднего, когда находится в апогее

своего эпицикла, и медленнее среднего, когда находится в перигее, так как планета неизбежно изменяет свое положение, в котором находилось бы Солнце, если бы не двигалось [по эпициклу].

Если движение центра эпицикла совершается по концентричному деференту 40 равномерно, то это — среднее движение [планеты], безразлично движется ли она, следуя движению своего эпицикла, или же совсем не движется. Движение планеты обладает избытком или недостатком [по отношению к среднему движению] потому, что она движется по своему эпициклу. Если планета находится на нижней стороне эпицикла, то кажется, что она движется назад. Центр эпицикла может также двигаться по эксцентричному деференту эксцентра, тогда его движение по деференту неравномерно. Из этого вытекает много аномалий.

Однако движение Солнца не может обладать аномалиями, обусловленными одной из этих двух гипотез — эксцентрической гипотезой при равномерных движениях и экциклической гипотезой при движении Солнца по эпициклу противоположно его равномерному движению по концентрическому кругу в сторону востока.

Птолемей выбрал первую гипотезу, так как ее легче предположить, а не из-за явной необходимости в ней. Он выбрал наиболее легкое из этих двух движений, потому что убедился в том, что при предположениях о некоторых условиях и предпосылках обе гипотезы одинаково соответствуют всему тому, что происходит на самом деле.

При каждой из двух гипотез необходимо иметь наименьшее и наибольшее расстояние. При эксцентрической гипотезе наибольшее расстояние находится в конце диаметра, проведенного через центры Земли и эксцентрического круга со стороны центра эксцентрического круга, а наименьшее расстояние — с другой стороны. При эпициклической гипотезе ясно, что [наибольшее расстояние находится в апогее эпицикла, а наименьшее — в его перигее]. Если планета находится в середине между этими двумя различными расстояниями и не смещается ощутимо к одному из них, то видимое движение будет равно движению центра эпицикла и являться средним движением.

Именно на наибольшем и наименьшем расстояниях имеет место предел аномалии; пределом аномалии считается наибольшая разность между средним и видимым [движениями]. Аналогичное наблюдается при эксцентрической гипотезе¹¹¹.

Мы утверждаем, что если имеются две равные дуги, одна из которых отложена от наибольшего расстояния, а другая — от наименьшего, то большим из двух углов, образуемых диаметром и линиями, проведенными из центра эклиптики к концам этих двух дуг, будет тот, который при наименьшем расстоянии.

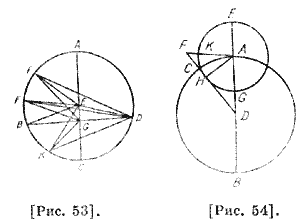
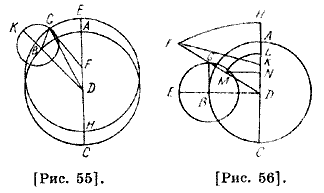
Что касается случая эксцентрической гипотезы, то пусть ABCD — эксцентрический круг [рис. 51], имеющий центр эклиптики Ε, DGEA — диаметр, проходящий через оба центра, и А — апогей, D — перигей; дуги АВ и CD — равные. Проведем ЕВ, ЕС, GB, GC. Поскольку углы АЕВ, DEC равные и угол АЕВ как внешний угол треугольника EGB больше угла EGB, то есть AGB, и поэтому угол DEC больше AGB. Следовательно, угол DGC как внешний угол треугольника CEG намного больше этого угла.

Что касается случая эпициклической гипотезы, то пусть ABC — концентрический [с эклиптикой круг], имеющий центр Ε и [полу]диаметр АЕ [рис. 52]; вокруг точки А опишем эпицикл, имеющий [полу] диаметр FA, пусть эпицикл движется от А, а светило — от G сторону В. Если светило находится в G или F, то оно не имеет движения, отличного от движения точки А, и если место светила 41 отлично от них, и оно проходит [дугу] GH, то опередит равномерное [движение] на дугу АН, а если проходит [дугу] GK, то отстает от равномерного движения на дугу АК, то есть на АН; GH больше FK, так как если через точку А проведем перпендикуляр к АЕ, то получится диаметр, который будет касательной к концентрическому [кругу] и отсекает в сторону G [дугу] меньше, чем отсекает концентрический [круг] ; время, за которое оно проходит [дугу] АН, больше того, за которое оно проходит [дугу] АК. Если оно движется противоположно этому движению, то все будет наоборот. Следовательно, его движения в равные [временные] дуги будут не равными, а различными. В первом положении при апогее движение медленнее, а в перигее — быстрее, а во втором положении, когда движение происходит по концентрическому [кругу], будет наоборот.

Таким образом, по эксцентрической гипотезе движение, которое кажется замедленным и меньшим, [происходит] при апогее, а то, [которое кажется] быстрым и большим, — при перигее. Что касается эпициклической гипотезы, то возможно и то и другое в соответствии с направлением движений светила в апогее: если они совпадают, то быстрее будет при апогее, а если противоположны, то быстрее — в перигее¹¹².

Докажем предположение о том, что все явления одинаково можно объяснить при случаях обеих гипотез, если выполняются следующие три условия: во-первых, чтобы линия, соединяющая оба центра, относилась к полудиаметру эксцентра как полудиаметр эпицикла к полудиаметру концентрического деферента; во-вторых, чтобы дуга деферента, пройденная центром эпицикла, была подобной [дуге] эпицикла, пройденной светилом за то же время; в-третьих, если направления двух движений при эпициклической гипотезе противоположны¹¹³ в квадранте, видимом от апогея.

Сначала мы докажем¹¹⁴, что при каждой из двух гипотез предел разности, вызванной неравенством, достигается, когда видимое [расстояние] от апогея составляет четверть [круга].

Пусть ABCD — эксцентрический круг вокруг центра Е, имеющий диаметр АЕС [рис. 53], центр Земли находится в G, проведен через него перпендикуляр BGD на диаметр, который разделит пополам эклиптику и вместе с общим диаметром составляет две четверти [круга]. Проведем ЕВ; АВ стягивает угол АЕВ истинного [движения], а угол AGB — видимого [движения].

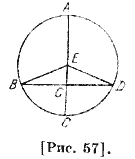
Отношение АВ из эклиптики к АВ из эксцентра — отношение этих углов, разность между этими углами и есть неравенство. Поскольку угол АЕВ внешний, который больше внутреннего угла G на угол В, то угол В — предел разности между средним и уравненным [движениями], являющийся избытком неравенства. Точно так же угол, ограничивающий разности между внешним и внутренним из различных центров, — это угол уравнения¹¹⁵. Мы утверждаем, что нельзя построить из внутренних линий в сторону В угол, не меньший, чем угол В. 42 Пусть построим угол F к апогею или угол К к перигею, проведем также линии ED, EF, DF, GF и GK; углы D и B в равнобедренном треугольнике DEB равны; точно так же углы D и F из треугольника EDF равны; DG, то есть GB, короче, GF, как было доказано в [„Началах"] Евклида, так как GF стягивает угол FDG, который больше GFD, то угол EFG меньше угла GDE, то есть GBE. Поскольку хорда GD, то есть GB, длиннее GK, то угол GKD больше угла GDK; но весь К равен всему D, значит, EDG, то есть EBG, больше EKG. Следовательно, угол В больше всех углов, находящихся на противоположных точках окружности¹¹⁶.

Тем самым доказано, что дуга АВ, соответствующая времени [перехода] от наименьшего движения к среднему движению, больше дуги ВС, соответствующей времени [перехода] от среднего к наибольшему движению при перигее; разность этих дуг есть дуга неравенства, соответствующая углу В, потому что угол АЕВ больше прямого на угол EBG, а ВЕС меньше прямого на тот же угол.

Докажем аналогичное в случае эпициклической гипотезы. Прежде чем приступить к этому, я утверждаю, что мы должны сначала знать, что как в истинном, так и в видимом [движениях] расстояние светила от апогея эпицикла не [равно] четверти круга. По-видимому, оно заключает в себе наибольшее неравенство, когда линия, выходящая из глаза до светила, касается эпицикла. Если же она пересекает его, то при этом расстоянии [светило] не имеет наибольшее неравенство, так как для каждой пересекающей [линии] можно найти такую точку [эпицикла] вне этой линии, при которой прямая линия, соединяющая ее с глазом, дала бы большее, чем то, расстояние от центра эклиптики. Таким образом, линия, проходящая через наиболее отдаленную точку от центра эклиптики, должна быть касательной. Но касательная через [точку] истинной четверти [с любой] из двух сторон параллельна диаметру эпицикла и поэтому не может дойти до глаза по прямой, так как глаз находится на диаметре. Поэтому касательная линия, проведенная из глаза, будет иметь другую точку касания. Если же соединить глаз с точкой той линии, что касается в [точке] четверти, то эта [линия] пересечет эпицикл, и поэтому может произойти пересечение до нее. Точка касания линии, проведенной из глаза, тоже должна доходить до [точки] пересечения эпицикла с концентрическим [кругом], так как если бы она была [точкой] этого пересечения и мы провели бы линию из центра эпицикла до нее, то угол, образованный у нее, был бы равен углу, образованному у центра диаметром, проходящим через оба центра, и линией, проведенной из центра эпицикла, поскольку обе стороны треугольника равны. Тогда [касательная] не была бы перпендикулярна [к диаметру], иначе в одном треугольнике имелись бы два прямых угла. Эта [точка] касания тоже не может быть дальше точки пересечения, так как если бы она была там, то угол, образованный [касательной] и полудиаметром эпицикла, был бы больше угла, который у центра, поскольку первый [угол] прямой. Тогда линия, соединяющая оба центра, была бы длиннее касательной, это нелепо, так как она равна ее части.

Далее угол, образованный касательной и диаметром эпицикла, прямой, и он больше того, который соответствует ему в случае пересечения. Также центральный угол в случае касания больше центрального угла в случае пересечения, так как этот [угол] при пересечении является частью того, [что при касании]. Поэтому третий [угол при касании] меньше, чем соответствующий ему 43 в первом случае. Таким образом, разность неравенства, к которой приводит этот угол в случае касательной, меньше другой разности неравенства. Это нелепо, так как это — угол предела неравенства. Итак, выясняется, что место [точки касания] — до пересечения эпицикла с концентрическим [кругом]. Отсюда доказывается, что дуга предела неравенства больше дуги, ограниченной центром эпицикла и [точкой] пересечения концентрического [круга с эпициклом] .

Пусть ABC — концентрический круг с центром D [рис. 54], EGH — эпицикл с центром A, BDGEA — диаметр, проходящий через эти центры, пусть точкой видимой четверти [круга] будет Н; допустим, что движение по концентрическому кругу разделит деферент на части, подобные частям, на которые разделится эпицикл движением светила. Угол ADC есть неравенство между средним движением при Ε и видимым движением при Н; по предположению, Η кажется находящейся на четверти [круга] . Угол D — предел разности неравенства и уравнения. Если DH — касательная, то АН обязательно пересекает ее перпендикулярно; восстановим из точки А перпендикуляр AF на диаметр. Избыток истинной четверти [круга] над К будет угол К АН, равный углу D; продолжим АК до встречи с DH; они пересекутся, так как сумма двух углов D и FAD меньше двух прямых, поскольку угол F — общий и угол А треугольника FAD равен углу Η треугольника HFA. Отсюда следует, что угол FAH равен углу D. Это разность неравенства.

Из всего этого следует, что дуга ЕН, которая определяет время [перехода] из наименьшего движения к среднему, будет больше дуги Н, которая определяет [время перехода] от среднего к наибольшему движению; разность между ними — удвоенная дуга КН, то есть [удвоенная] дуга АС, так как эти дуги подобны между собой.

Разность есть удвоение этого, так как одна из них меньше истинной четверти на эту [величину], а другая больше ее на эту [величину].

Из этого также доказывается, что при обеих гипотезах движение подобно среднему [движению] и совпадает с ним, когда достигается предел разности неравенства. Однако обе гипотезы совпадают не только в [рассмотрении] предела неравенства, а также частных неравенств для частных дуг. Поэтому если соблюдать [условия] предпосылки, то уравнение будет одним и тем же за равные [промежутки] времени, под уравнением имеется в виду разность неравенства. Это имеет место независимо от того, будет ли [указанное] отношение одним и тем же при обеих [гипотезах], которое произойдет, если полудиаметр эпицикла равен линии, соединяющей оба центра, или же это отношение подобно, то [есть] полудиаметр эпицикла относится к линии, соединяющей [оба центра], как полудиаметр концентрического [круга] к полудиаметру эксцентра.

Сначала положим, что отношение одинаковое. Пусть ABC — концентрический круг [рис. 55], имеющий центр в D; GK — эпицикл с центром В. EGH — эксцентр с центром F; общий диаметр концентрического круга и эксцентра EDC: когда центр эпицикла отсекает АВ, то светило отсекает KG, подобную АВ. Соединим FG, DG 44 и BG. Поскольку FD и GB по предположению равны, то FG и DB также равны, так как получается параллелограмм, угол FGD, который является разностью неравенства по эксцентрической гипотезе, равен накрест лежащему GDK, который представляет собой разность неравенств по эпициклической гипотезе. Внутренний угол ADB равен внешнему одностороннему с ним AFG; GBK также внешний угол, поэтому дуги треугольника подобные. Следовательно, место светила в них одно и то же; разность неравенства в них одна и та же при одинаковом времени. Ясно, то же самое получится для любых дуг.

Что касается доказательства при случае, когда это отношение подобное, то пусть ABC — [круг] деферента, имеющий центр D [рис. 56], a EG — эпицикл, имеющий центр В, пусть эпицикл отсекает АВ, а светило отсекает EG, подобную АВ; проведем круг эксцентра больший, чем деферента, это круг HF с центром К, а также меньший его, это Μ с центром N. По условию полудиаметр эпицикла относится к линии, соединяющей центры, как полудиаметр деферента к полудиаметру эксцентрического [круга]. Проведем BG, а также продолжим GD, проходящую через Μ дуги LM до F — из дуги FH; продолжим DB до Е, то есть до апогея.

Мы утверждаем, что все эти дуги подобные. Поскольку GE подобна АВ, то угол GBE равен углу ADB; BG и DА параллельны; угол BGD треугольника GDB равен накрест лежащему, угол D — общий для треугольников MDN и FKD, их стороны, содержащие этот угол, пропорциональны, так как стороны DG и BD пропорциональны их сторонам. Поскольку отдельные углы равны и содержащие их стороны пропорциональны, то BG относится к DG как DΚ к KF; по предположению отношение BG и DK равно отношению DA к FK и отношению DG к DF; таким образом, соответственные углы в треугольниках равны, то есть углы GDB, DFK и DMN равны; линии BD, MN и FK параллельны, следовательно, углы ADB, HKP и LNM равны, поэтому их дуги будут подобными. Итак, светило будет усматриваться по одной и той же прямой DMGF, при этом оно будет казаться находящимся соответственно в точках F, M и G.

Мы утверждаем также, что когда в видимом движении [светило] пройдет равные дуги от наибольшего и от наименьшего расстояния, то в обоих положениях происходящее от неравномерности видимое неравенство будет одинаковым, потому что, когда [светило] находится в стороне апогея, уравнение уменьшается, а когда в стороне перигея — возрастает. Такое же наблюдается 45 при обеих гипотезах. Докажем это по эксцентрической гипотезе. Проведем из центра Земли G какую-нибудь [рис. 57] [линию], пересекающую диаметр, перпендикулярно, пусть это DGB, которая неизбежно отсекает равные видимые дуги DC и АВ, потому что [стягиваемые ими] углы как вертикальные равны; соединим D и Ε, Ε и В; ясно, что углы D и В равны в силу равнобедренности [треугольника], но угол DEG меньше внешнего BGC, который соответствует неравномерному движению при перигее и [меньше] угла DGC на угол D, а угол AGB при апогее, который равен DGC при перигее, [меньше AЕВ] на угол D. Это есть разность между видимым и средним [движением], каждый из равных углов В и D есть разность между видимым и средним [движением].

Согласно этому среднее [движение] иногда больше видимого исправленного, а иногда меньше его. Однако они равны. Следовательно, прибавляемое и вычитаемое в них одинаковы. Что касается случая эпициклической гипотезы, то пусть этими двумя дугами в эпицикле будут произвольно взятые дуги EG и HF, которые отсекаются одной и той же линией, выходящей из D и являющейся центром концентрического [круга]. Известно, что по видимости они равны, то есть вызывают одно и то же неравенство, потому что разность неравенства, то есть угол D, для них обоих один и тот же. Но эти дуги различные. Соединим А и Н, А и G, тогда угол Ε AG больше AGD на угол ADG, AHG больше внутреннего DАН на угол D; но, как было доказано, угол G — это угол видимого движения в апогее, потому что он — разность между ним и внешним углом, EAG есть то, что соответствует среднему, то есть углу D. Таким образом, угол G меньше угла EAG, соответствующего среднему [движению], на угол D.

Что касается перигея, то угол видимого движения при нем — угол AHG, равный углу AGH, больше среднего угла, соответствующего FAH, также на угол D, а в действительности меньше ЕАС также на угол D. Следовательно, среднее движение в наибольшем расстоянии будет больше видимого на такой угол, на который меньше оно в наименьшем расстоянии от видимого, если указанное отклонение будет точно таким же.

О видимом неравенстве движения Солнца

Птолемей исследует неравенства [движения] Солнца. Он говорит: хотя возвращения Солнца происходят за [равные] промежутки времени, однако обнаруживается, что оно не проходит четверти [эклиптики] за равные времена; поэтому оно не переходит дуги, меньшей четверти, за равные [промежутки] времени. Следовательно, видимое движение Солнца неравномерное. Однако его неравенство наблюдается в одних и тех же местах. Для его [объяснения] предпочтительно привлечь эксцентрическую гипотезу. Поэтому необходимо найти правило [нахождения] его уравнения по этой гипотезе.

Сначала определим величину соединяющей линии и место наибольшего расстояния в эклиптике. Гиппарх на основе наблюдений нашел, что время [движения] от весеннего равноденствия до летнего солнцестояния — девяносто четыре и половина 46 дня, а от этого солнцестояния до осеннего равноденствия — девяносто два с половиной дня¹¹⁷. Используя эти данные, он вычислил, что соединяющая линия (эксцентритет) составляет двадцать четвертую часть полудиаметра эксцентра; [точка] наибольшего расстояния предшествует [точке] летнего солнцестояния примерно на 24; 30 градуса, отсюда вытекает, что в этой четверти движение несколько замедленное.

Птолемей, исходя из метода Гиппарха, по-своему доказывает указанное явление в соответствии со своими наблюдениями. Он нашел по наблюдению, что время от осеннего до весеннего равноденствия равно 178 и одной четверти дня, а от весеннего до летнего солнцестояния 94 с половиной дням. Из этого следует, что апогей и отношение линий соответствуют тому, что было приведено Гиппархом.

Пусть ABCD — круг Зодиака с центром Ε [рис. 58], FKLM — эксцентрический круг с центром G, А — [точка] весеннего равноденствия, а В — летнего солнцестояния; из точки G проведем линию NGO, параллельную АС, которая пересекает BD в X; линия PG, параллельная BD, пересекает АС в Q. Поскольку GN выходит из центра, a QF — из другой точки диаметра BG, то GN длиннее ее; проводим перпендикуляр FX на GN, который будет параллельным DB и пересекает [GN] внутри круга и отсекает GX, равную QF; его продолжим до T, в X [линия] FT разделится пополам.

Точно так же проведем КС, которая в С разделится пополам; тогда точки F, К, L и Μ являются точками четверти в эксцентрическом [круге], [точка] F, которая видна по направлению А, соответствует [точке] весеннего равноденствия, а К, соответствующая точке В, — [точка] летнего солнцестояния. Аналогичное наблюдается и с остальными точками.

На основе наблюдений Птолемей определяет период прохождения [Солнцем] дуги KLM, следовательно, находит части среднего движения, что КМ меньше полукруга и равна удвоенной дуге ОК, что КО — ее половина, определяет, насколько она меньше четверти [круга], и находит ее меньшей на дугу КР, но КР — известна; по наблюдению Птолемей находит KF и поэтому КР известна, определяет FN — избыток над четвертью.

Продолжим линию, соединяющую центры до эклиптики, это EGH; поскольку движение замедленное в северной половине, из двух квадрантов на KF окажется апогей, который находится в точке Я; поскольку дуга FN известна, то ее половина FT и ее хорда FXT известны, ее половина FX известна: точно так же КС известна, следовательно, параллельные с ними QG и GX известны; таким образом, четыре стороны ЕХ будут известными и поэтому диагональ (хорда прямого угла) известна, то есть соединяющая линия известна; центральные углы известны из треугольника; это угол АЕН, то есть дуга АН известна. Таким образом, определено отношение соединяющей линии к полудиаметру деферента; определяется расстояние апогея от [точки] весеннего равноденствия и, следовательно, квадранты эксцентрического круга будут известными.

Таким образом, найдены место апогея и отношение соединяющей линии согласно тому, что было у Гиппарха¹¹⁸.

Птолемей утверждал, что апогей Солнца неподвижен и не перемещается. Что касается позднейших [ученых], то наблюдения, проведенные во времена Мамуна¹¹⁹ тем же методом, показали, что апогей Солнца отклоняется от места, указанного Гиппархом 47 по отношению к движению неподвижных звезд. Это же установили и мы по своим наблюдениям, [произведенным] после сочинения этой книги¹²⁰.

Далее он показывает, что предел неравенства достигается при девяносто двух градусах и двадцати трех минутах от апогея эксцентрического круга или эпицикла. Сначала это докажем при эксцентрической гипотезе. Он сказал: пусть из центра эклиптики Ε восстановим перпендикуляр на диаметре и [продолжим его] до точки В [рис. 59]. Соединим В и D. По доказанному этот угол DBE соответствует пределу разности, обусловленной неравномерностью [движения], стороны треугольника BED известны, потому что известно отношение BD к DE по предыдущему предложению; угол Ε — прямой, остальные углы известны, то есть угол В известен по вычислению. [Предел неравенства] составит два градуса двадцать три минуты¹²¹, каких в четырех прямых содержится 360 градусов; ADB как внешний угол известен и поэтому дуга АВ известна по вычислению вышеуказанным [способом], она больше прямого [угла] на предел неравенства.

Что касается случая эпициклической гипотезы, то пусть ABC — концентрический круг, BEG — эпицикл с центром А [рис. 60], DG — касательная, проведенная из центра, тогда А обязательно перпендикулярна к ней; отношение AG и ΑD известно по треугольнику, стороны и углы по указанному нами способу будут [также] известными; поэтому угол D известен, то есть дуга разности известна, внешний угол EAG через два угла треугольника известен; следовательно, дуга EBG, то есть расстояние от апогея, известна. Результаты вычисления соответствуют указанным выше.

Об определении частных [значений] неравенств

Что касается того, как можно определить эфемериды [движений] Солнца, то мы утверждаем, что когда определим расстояния среднего движения от апогея, то мы определим и то, что приходится на долю неравенства, и узнаем местонахождение [Солнца] в эклиптике.

Сначала докажем это в случае эксцентрической гипотезы; пусть ABC — концентрический круг [рис. 61] с центром D; EGH — эксцентрический [круг] с центром F; пусть дуга EG известна; соединим F и G, D и G; [дуга] АВ из эклиптики и есть искомая [величина], она видна из [центра эксцентра] по дуге GE.

Продолжим GF до К, то есть до основания перпендикуляра DΚ, проведенного из центра; таким образом, угол К и угол KFD как вертикальный с известным углом EFG будут известными; FD как диаметр описанного около [прямо угольного] треугольника [FKD] известен; тогда стороны и углы этого треугольника по тому, что было сказано, будут известны¹²², следовательно, FD как одна из сторон известна, таким образом, KF и FG известны по отношению и поэтому KG известна и KD 48 известна ; К — прямой угол, отсюда DG известна и угол разности [неравенства], то есть угол G, известен; углы FDG и KDF известны; следовательно, угол ADG известен и [искомая дуга] АВ известна ; если положить EG равной тридцати градусам, то АВ будет равна 28,51 градуса.

Мы утверждаем также, что если считать известным угол дуги эклиптики или угол разности, то и другие из указанных углов будут известны. Предположим, что угол D известен; опустим перпендикуляр FL на DG [рис. 62]. Поскольку углы D и L прямоугольного треугольника FDL известны, то DF известна по отношению к FL, в треугольнике стороны и углы треугольника известны по тому же отношению; отношения DF к FG и FD к FL известны, угол L — прямой и LG известна из известного треугольника FLG, все углы известны, угол G, равный разности неравенства, известен, внешний угол EFG и [дуга] EG известны.

И пусть на этом же рисунке угол G известен, гипотенуза FG также известна. В треугольнике FGL известны стороны и углы, отсюда треугольник FLD будет известным по двум сторонам и прямому углу; следовательно, угол D, внешний угол F и дуга EG известны. Что касается доказательства этого в случае эпициклической гипотезы, когда известна дуга от апогея, то пусть ABC — концентрический круг с центром D [рис. 63], a EGHF — эпицикл с центром A; D соединим с точкой апогея А, допустим EG — известна и пусть она составляет тридцать градусов; соединим G и A, D и G; опустим перпендикуляр GK на DE; углы GAK и GKA известны, GA известна; все стороны и углы треугольника будут известными; тогда AD будет известна в отношении к AG. Таким же образом находится и АК, отсюда KD будет известна, а угол К — прямой и поэтому KG известна, так как из треугольника GKD будет известен угол D. Получается тот же результат, что и в случае эксцентрической гипотезы.

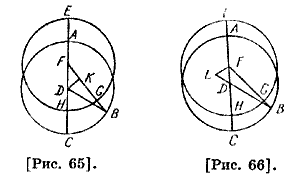
Теперь докажем в случае эпициклической гипотезы и обратное. Пусть известен угол G, который соответствует дуге от [точки] весеннего равноденствия по эклиптике, которое известно; опустим перпендикуляр AL на DG [рис. 64], угол L прямой, линия AG и угол G известны; линия AL известна из треугольника; в треугольнике ALD углы будут известными, так как угол D — данный, следовательно, угол GAE и дуга EG будут данными. Пусть угол D известен, тогда, по аналогичному рассуждению, треугольник DAL будет известным, и поэтому AL и AG известны, угол ALG — прямой; поскольку сторона и два угла известны, то и угол G известен; отсюда также угол GAE и поэтому дуга EG будут известны; вычисление вполне согласуется с тем, что было выше. Это все, что касается дуг в сторону апогея.49

Затем рассмотрим дуги в сторону перигея, для которой берем квадрант из другого рисунка [рис. 65]. Пусть Η — известная дуга, отложенная от перигея, которую мы примем равной тридцати градусам; соединим F и G, D и G, продолжим F до В, опустим из D на FG перпендикуляр DK, который известен; аналогично тому, как мы уже доказали, треугольник FDK будет известным, угол К — прямой; в треугольнике DKB также известны углы и стороны, и поэтому в треугольнике FDB будет известен угол ВВС, то есть дуга ВС известна.

С другой стороны, если дается угол, то будем считать угол D известным, опустим перпендикуляр из F до встречи с [продолжением] GD [рис. 66] в точке L; тогда по доказанному выше стороны и углы треугольника FLD будут известными; точно так же и в треугольнике FLG, FDB и оставшийся угол GFH известны; угол G положим данным, то есть разность неравенства известна, угол L — прямой, тогда линия GF и треугольник известны по отношению, а также FL и FD известны, угол L — прямой, поэтому стороны и углы треугольника FLD известны; отсюда угол FDL, то есть угол BDC и дуга ВС известны, и угол GFI1, то есть дуга GH, известны.

Пусть теперь это же самое докажем в случае эпициклической гипотезы; пусть сначала будет известна [дуга] HF со стороны перигея [рис. 67], опустим перпендикуляр HК на DА. Поскольку НА и угол А дуги HF известны и угол К прямой, то известны углы и стороны треугольника АНК; по доказанному прежде углы и стороны треугольника KHD известны; угол D и дуга АВ известны.

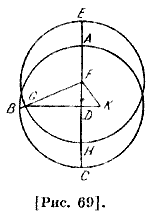
Что касается того, когда дается угол, то пусть сначала положим видимый угол в эклиптике известным; опустим перпендикуляр AL на DB [рис. 68], АHВ — видимый угол в эклиптике, потому что он соответствует среднему [движению] и по предположению уравнение известно; тогда два треугольника 50, то есть треугольник ALH по известной стороне АН и углам L и H и треугольник ALD по известным двум сторонам AL и AD, известны, следовательно, угол D известен.

А теперь пусть угол D будет известным; тогда углы и стороны треугольника ALD будут известными по известной стороне и известным углам D и L, который прямой; также стороны и углы треугольника ALH будут известными по двум сторонам — AL и LH и прямому углу L, и, следовательно, искомый угол HAF известен.

Далее, после того, как был указан способ нахождения неравенств, чтобы иметь их готовые значения, Птолемей составил таблицу неравенств для частных дуг¹²³. При этом поскольку он доказал, что разность неравенства в другой половине равна соответствующему в этой половине и прибавляемые величины в одной из них будут вычитаемы в другой, он ограничился неравенством, имеющим место [только] в одной половине между двумя указанными расстояниями.

Так как для дуг, примыкающих к наибольшему расстоянию, неравенство меньше, то он разделил прилегающий к этому квадрант на пятнадцать частей, каждая из которых соответствует шести [градусам], и поместил их неравенства. Поскольку для квадранта, прилегающего к наименьшему расстоянию, неравенство больше, то его разделил на тридцать частей, каждая из них соответствует трем [градусам]; поэтому он принял эти числа через каждые три [градуса].

В первом столбце содержится число, соответствующее движению от апогея, во втором — число, соответствующее движению от перигея. В третьем — целые числа градусов и минут прибавляемого и вычитаемого неравенства; они прибавляются, если среднее берется из второго [столбца], и вычитаются, если— из первого [столбца].

Далее он требует [установить] эпоху среднего движения Солнца, которая начинается с середины первого дня царствования Набонассара, и эпоху Солнца в тот день истории. Он показал среднее положение Солнца в двух осенних равноденствиях, наблюденных из наибольшего расстояния, как на этом рисунке [рис. 69].

Он сказал: пусть G — точка осеннего [равноденствия] в эксцентрическом [круге], Η — его перигей; опустим перпендикуляр FK к GD дуга СВ круга эклиптики известна, потому что она — расстояние [точки] осеннего [равноденствия] от перигея; тогда угол избытка, то есть [угол] G, известен. Отсюда следует, угол [H]FG также будет известным. С помощью вычисления получается, что дуга HG равна 63; 20.

После определения среднего [движения] Солнца он нашел промежуток времени между настоящим наблюдением и началом эпохи, 51 установил число полных оборотов за это время, отбросив их, нашел прибавляемую дугу и ее начало на эксцентрическом круге; это есть среднее положение Солнца в начале эпохи. Уточнив это, он узнал, как находятся эфемериды Солнца.

Он сказал: среднее [движение] Солнца находится с помощью определения промежутка времени с начала эпохи; к этому прибавляется эпоха и отнимаются полные обороты до градуса апогея; остаток берется в столбце среднего [движения], затем находится соответствующее ему уравнение, которое прибавляется или отнимается по тому [правилу] , о котором мы уже сказали.

Из всего этого выясняется, что положение Солнца может быть получено с помощью геометрических доказательств; причем это не зависит от того, предполагается ли, что эклиптика равна эксцентрическому кругу или же больше него, ибо рассматриваются углы у центра эклиптики и треугольники, имеющие углы, общие для обоих кругов — равного эксцентрическому или больше него; если они у центра круга, [не] равного [эксцентрическому], то дуги подобны.

О неравенствах суток

Далее, когда Птолемей разъяснил обстоятельства Солнца, он закончил эту книгу разъяснением [вопроса] о сутках.

Он сказал: судя по тому, что видно, можно думать, что сутки — это поворот [небесного экватора] на триста шестьдесят градусов, и это двадцать четыре часа. Это период возвращения точки небесного экватора, восходившей вместе с Солнцем в первый день или бывшей вместе с ним в полдень, к линии горизонта

или к линии меридиана. При этом предпочитается меридиан, так как периоды возвращений к нему равны во всех климатах. Именно так думают вообще об этом вопросе. Но истинные сутки — это время возвращения Солнца к кругу горизонта или небесного меридиана, а Солнце проходит за сутки средним движением приблизительно 59 минут. Следовательно, период возвращения Солнца превышает период возвращения той точки, которая была [вместе с ним], так как оно отстает от нее. Поэтому средняя [продолжительность] суток 360 временных градусов и 59 минут, а это — двадцать четыре часа и пятьдесят девять девятисотых часа. Однако, как было сказано выше, движение Солнца неравномерно, приращение движения Солнца по эклиптике не одно и то же и равные приращения по эклиптике имеют не одни и те же временные градусы восхождения и прохождения небесного меридиана. Следовательно, существуют два вида неравенств суток. Хотя это неравенство не имеет [существенной] величины при малом числе суток, оно обладает ощутимой величиной, когда число суток увеличивается.

Поскольку предел разности, возникающей из-за аномалии [движения] Солнца, наблюдается там [между положениями], в которых движение равномерно, [в них] разность незаметна. Промежуток времени между каждым из двух противоположных расстояний и этой точкой [равномерного движения] приводит к наибольшему уравнению, а наибольшая разность имеет место с другой стороны, в противоположном направлении. Поэтому промежуток времени со стороны апогея избыточен и уравнение вычитается, а [промежуток времени] со стороны перигея недостаточен, уравнение прибавляется и достигает двух градусов двадцати трех минут. Удвоение этого дает разность между равномерным и неравномерным движением приблизительно в четыре и три четверти градуса. Одна половина эклиптики отличается от другой на удвоение этого удвоения, то есть на девять с половиной градусов. Поэтому количество суток при движении от середины до середины будет отличаться от [количества] средних суток на четыре и три четверти градуса. На такую же величину вместе все избыточные и все недостаточные сутки отличаются от средних суток. Поэтому длинные сутки отличаются от коротких на удвоенную [величину], то есть 52 на девять с половиной градусов. Это наибольшая разность по причине Солнца.

Что же касается наибольшей разности по причине восхождений, то ее надо рассматривать или по отношению к горизонту, или по отношению к середине неба. Если рассматривать ее по отношению к восходам и заходам на горизонте, то в большинстве стран наибольшая разность отличается в двух половинах [эклиптики], разделенных двумя солнцестояниями. Каждая половина эклиптики отличается от средней величины на разность между наибольшим и средним днями, то есть вдвое больше нужной. Это соответствует разности между наибольшим и наименьшим днем в зависимости от климата.

[Если же рассмотреть] ее по отношению к прохождению середины неба, то имеется только одно неравенство наибольшей разности, к которому приводят восхождения. Неравенство разности восхождений не изменяется в [различных] климатах. Предел его уменьшения имеет место между серединой Водолея и началом Скорпиона, а предел увеличения — между началом Скорпиона и серединой Водолея. Разность неравенства вместе с уравнением составляет четыре с половиной градуса. В этом же самом месте доля наибольшей разности изменения движения Солнца составляет приблизительно три и две трети градуса. Складывая их, получим восемь и одну треть градуса. Это сумма двух неравенств вместе с уравнением. [Разность же] между наибольшим и наименьшим числами вдвое больше. Это не изменяется в различных климатах.

За начало эпохи принимается не начало дня, а полдень, так как разность в нем одна и та же, где бы это ни было, а по отношению к горизонту она изменяется в зависимости от знака Зодиака, даты во всех странах не совпадают.

Разность, полученная пои соединении этих двух [разностей] — разности от движения Солнца и от неравенства его прохождения через середину неба, то есть того, что следует прибавить или вычесть, вместе составляет восемь и одну треть временных градусов или половину и одну восемнадцатую часа. Это потому, что прибавление происходит от Скорпиона до середины Водолея, а вычитание — от Водолея до Весов. Следовательно, наибольшая разность, определяемая неравенством [движения] Солнца, — три и две трети градуса, а [наибольшая разность, определяемая] прохождением [Солнца] через середину неба, — приблизительно четыре и две трети временного градуса. Это получается, если восхождения и уравнение Солнца сложить, так чтобы получилась наибольшая [величина]. Если это так, то сутки превысили бы друг друга на половину этой наибольшей разности и получилось бы шестнадцать и две три временного градуса, или один и одна девятая часа. Эта величина не приводит к большим изменениям Солнце и другие [планеты]. Но для Луны получается ощутимая разность, близкая к трем пятым градуса.

Далее он сказал о сутках и их установлении: сутки начинаются с полудня или с полуночи; находим положение Солнца в начале их и берем истинное и среднее [значения положения Солнца]. [Затем] находим восхождение в прямой сфере между двумя истинными [значениями] и выражаем разность в часах. Если восхождение превышает средние солнечные сутки, то прибавляем эти часы; если лее они меньше, то вычитаем их; то, что получится, — есть истинные сутки. Таким же способом поступаем в случае сложенных средних равномерных движений.

53 С помощью этого метода мы можем перейти и обратно от временных суток к средним равномерным.

Затем он упорядочил положение Солнца относительно начала его эпохи. Оказалось, что при среднем движении оно на 0;45 градусе Рыб, а в истинном [движении] — на 3;08 [градусах].

Комментарии

95. Третья книга «Альмагеста» состоит из следующих глав:

О продолжительности годового промежутка времени.

Таблица средних движений Солнца.

О предположениях, касающихся равномерного кругового движения.

О видимом неравенстве Солнца.

О составлении таблиц неравенства на отдельных участках.

Таблицы солнечной аномалии.

Об эпохе среднего движения Солнца.

О вычислении положения Солнца.

О неравенстве суток.

96. О целях этой книги «Альмагеста» Птолемей пишет: «Изложив в предыдущем сочинении совершенно необходимые математические сведения о небе и земле, о наклонности проведенного через середины зодиакальных созвездий солнечного круга, о связанных с нею частных явлениях на прямой сфере, о наклонной для каждого климата, мы полагаем, что после этого следует изложить теории, касающиеся Солнца и Луны, а именно исследовать все, происходящее при их движениях, так как без предварительного исследования, изложенного выше, никакое явление, относящееся к светилам, не может быть изучено. В дальнейшем мы должны прежде всего получить теорию солнечного движения, без которой, в свою очередь, невозможно полностью охватить все, касающееся Луны» [3].

97. Птолемей в «Альмагесте» не дает общего определения среднего движения для всех светил, то есть Солнца, Луны и пяти планет.

98. Эфемериды — таквим (буквально — «исправление», этот же термин означает и календарь). Наш термин «эфемерида» происходит от греческого слова, означающего «дневник, запись на каждый день».

99. Аль-Фараби дает общий для Солнца, Луны и планет способ нахождения периода среднего движения и тем самым существенно дополняет содержание соответствующей главы «Альмагеста», которая сразу же начинается с определения продолжительности годового промежутка времени.

100. Аль-Фараби здесь считает нужным более подробно описать этот инструмент (зат аль-халык), тогда как в соответствующем месте «Альмагеста» мы читаем о нем всего несколько фраз, якобы принадлежащих Гиппарху: «Вообще же неравенства годовых промежутков могут быть точно установлены при помощи наблюдений на установленном медном кругу в так называемом квадратном портике; на этом кругу равноденствие, видимо, отличается тем, что его вогнутая поверхность начинает освещаться с обеих сторон».

101. Алидада — идада — буквально «сторона линейки» — подвижная линейка в астролябии и других угломерных инструментах (слово «алидада» — транскрипция слова аль-идада).

Диоптры — два приспособления с отверстиями, прикрепленные к алидаде, с помощью которых она направляется на данный объект.

102. Таким образом, время оборота Земли вокруг Солнца — тропический год, т. е. промежуток времени между двумя весенними равноденствиями, равен

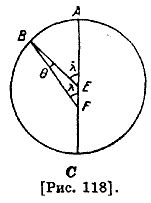
103. Метон — греческий астроном, работал в Афинах. Открыл 19-летний цикл в 432 г. до н. э.

104. Евктомен — греческий астроном, сотрудник Метона, занимался наблюдением солнцестояний.

105. Аристарх Самосский (около 300 г. до н. э.) — великий астроном и математик древности, впервые выдвинувший гипотезу о вращении Земли и движении ее и планет вокруг Солнца.

106. Симак Безоружный — звезда Спика, т. е. α созвездия Девы.

107. Эту таблицу мы привели в приложениях к данной работе (таблица 5).

108. Кажущаяся аномалия Солнца и других светил — неравномерность видимого движения этих светил по эклиптике. Древнегреческие астрономы вслед за Аристотелем исходили из предположения о том, что Солнце и все светила равномерно обращаются вокруг Земли, исключение составлял только Аристарх Самосский. Неравномерность движения Солнца объясняется одной из двух эквивалентных гипотез: эксцентрической или эпициклической (см. прим. 109, 110). Движение Луны и планет объясняется с помощью комбинации этих гипотез.

109. Согласно эксцентрический гипотезе, неравномерность видимого движения Солнца по небесной сфере объясняется тем, что оно движется равномерно по некоторому кругу, расположенному в плоскости эклиптики (плоскости видимого движения Солнца), но эксцентрично к ней. На рисунке 118 ABC— эксцентрический круг, Ε — его центр, F — центр мира (центр Земли), А — апогей (аудж) Солнца, т. е. его наибольшее расстояние от наблюдателя, D — его перигей (хадид), т. е. наименьшее расстояние, В — одно из положений Солнца. Угол EBF=θ — называется «уравнением» Солнца или его «поправкой».

110. Согласно эпициклической гипотезе, Солнце вращается по небольшому кругу — эпициклу, центр которого обращается вокруг Земли по большому кругу — деференту, а его центр совпадает с центром Земли. Эпицикл — фалак тадвир, буквально «орбита приведения во вращение», деферент — фалак аль-хамил, дословно «несущая орбита».

111. Комментарии аль-Фараби сущности двух гипотез более общи и подробны, чем объяснения в тексте «Альмагеста», в котором читаем следующее: «Причины же кажущейся неравномерности можно объяснить главным образом двумя первоначальными и простыми гипотезами. Действительно, если их движение усматривается происходящим по имеющей один центр с миром окружности, находящейся в одной плоскости с кругом, проходящим через середины зодиакальных созвездий, и наш глаз без большой погрешности можно считать находящимся в центре мира, то для объяснения неравномерности следует допустить, или что они совершают равномерные движения не вокруг центра, или же хотя и вокруг этого центра, но не просто по этим окружностям, а по перемещаемым ими другим окружностям, называемым эпициклами. Какую бы из этих гипотез мы ни приняли, окажется, что для наших глаз в одинаковые промежутки времени они будут проходить неодинаковые дуги по окружности, проходящей через середины зодиакальных созвездий и имеющей один центр с миром» [3, стр. 152].

112. Последнее доказательство отсутствует в «Альмагесте», по-видимому, оно добавлено аль-Фараби.

113. Это не что иное, как теорема кинематики о паре вращений, принадлежащая Аполлонию Пергскому (около 200 г. до н. э.), которая в переводе на язык древней астрономии означает, что система эпицикла и деферента, при условии равных и противоположно направленных вращений, эквивалентна неподвижному эксцентру [13, стр. 87— 90].

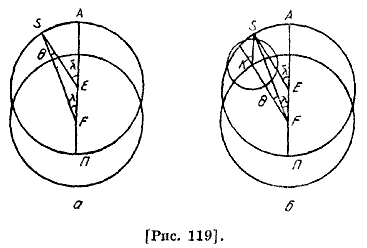
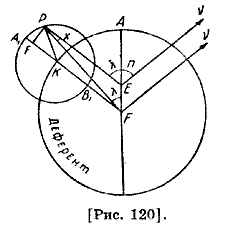
Поясним совпадение видимого движения Солнца при эксцентрической и эпициклической гипотезах [рис. 119, а, б]. На рисунке 119, б за деферент принята концентричная орбита с центром в центре мира. Пусть F — центр мира, Ε — центр эксцентра, А и Π — соответственно апогей и перигей эксцентрической орбиты, S — Солнце, λ' — средняя долгота Солнца (средний аргумент), λ — его истинная долгота (уравненный аргумент), θ — уравнение Солнца, α — аномалия Солнца. Чертежи 119 а, б наглядно показывают совпадение λ, λ' и θ при обеих гипотезах.

114. Дальше в «Альмагесте» даются следующие разъяснения, которые аль-Фараби не приводит здесь, так как он во введении к этой главе предпослал общие объяснения движениям светил (в том числе Солнца): «... и что время движения от апогея до упомянутого среднего положения будет дольше времени движения от этого среднего положения до перигея. Отсюда получается, что при гипотезе эксцентров всегда, а при гипотезе эпициклов тогда, когда перемещения светил от апогея идут в направлении против последовательности знаков, время перехода от места с наименьшим движением к среднему будет больше времени движения от места со средним движением к месту с наибольшим движением, так как при каждой из этих гипотез наименьшее движение получается в апогее; при гипотезе же эпициклов, когда движения светил по эпициклам производятся от апогея в направлении последовательности знаков, наоборот, время движения от места с наибольшим движением к среднему будет больше времени движения от места со средним к месту с наименьшим движением, так как в этом случае апогею будет соответствовать наибольшее перемещение».

115. Уравнение (тадил) или поправка — важное понятие в теории движения светил. Угловые расстояния, отсчитываемые в эклиптике при центре (Птолемей называет эту точку «глаз наблюдателя или центр круга, концентричного с эклиптикой») от некоторой определенной его точки [рис. 120] — точки весеннего равноденствия, получили название долгот. νEA, равная νFA, есть долгота апогея; обозначим ее через π; угол νFP есть видимая долгота светила, которую обозначим λ, от нее отличают среднюю долготу, определяемую направлением на центр эпицикла.

Долготы считаются в эклиптике в направлении видимого годичного движения Солнца, от запада к востоку (это направление и считается прямым), каждые 30° долготы соответствуют одному «знаку Зодиака». Вступления Солнца в знаки Овна, Рака, Весов, Козерога, т. е. моменты, когда его долгота равна 0, 90, 180, 270°, означают начала времен года. Таким образом, y=π + λ, где угол λ равен углу AFP, которым (поскольку π сохраняет постоянное значение) измеряется неравномерное движение светила, воспринимаемое наблюдателем: найти закон изменения его с течением времени — основная задача теории светил; для этого требуется связать угол λ с каким-либо равномерно возрастающим углом. В этой схеме эта связь осуществляется следующим образом. Продолжим радиус деферента FK до пересечения с эпициклом в точке А₁. Эта точка и противолежащая ей Β₁ — так называемые истинный апогей и истинный перигей. Угловое расстояние светила от истинного апогея, т. е. угол А₁КР, равный углу PEA, есть, по Птолемею, аномалия планеты, мы будем обозначать ее через λ'.

Таким образом, задача заключается в том, чтобы найти выражение λ через λ', но имеем: λ=λ'—x, обозначая через x угол EPF=PFK, то есть тот угол, под которым наблюдатель усматривает радиус эпицикла или под которым из Ρ усматривается эксцентриситет эксцентра FE. Углы, отсчитываемые при центре деферента F, назывались в средние века центрами: угол AFK, равномерно возрастающий, есть средний центр (centrum medium); угол x — периодическое неравенство или уравнение этого центра (aequatia centri), поэтому λ есть центр, отягченный его неравенством [13, стр. 92—93].

116. Здесь геометрически доказано утверждение о том, что наибольшее значение уравнения центра соответствует значению λ=90°.

В нашей записи из соотношения sin x=e sin λ, которое легко можно получить из треугольника PEF при λ=90°, мы имеем sin x_max =е, где е — эксцентриситет эксцентра.

117. Одним из кардинальных фактов в теории Солнца древних является установление того, что внутри года наблюдаемое движение Солнца не остается равномерным: равные углы по видимой долготе Солнце проходит в неодинаковые интервалы времени. Так, астрономическая весна (промежуток, когда видимая долгота Солнца возрастает от 0 до 90°) длится 94,5 дня; астрономическое лето (промежуток времени, когда видимая долгота увеличивается от 90 до 180°), составляет 92,5 дня.

На трех данных — на величине среднего суточного движения μ и на длине весны и лета — Гиппарх, а за ним и Птолемей строят теорию Солнца, которую и излагает по-своему аль-Фараби.

118. Гиппарх получал П=65°30'; е=¹/₂₄.

119. Аль-Мамун — багдадский халиф, правивший в 813—833 г., покровитель наук в арабском Халифате. При дворе аль-Мамуна работали аль-Хорезми, аль-Мервази, аль-Джаухари, аль-Фергани, уроженцы Хорезма, Мерва, Фараба и Ферганы.

120. В связи с определением долготы апогея Солнца аль-Фараби здесь затрагивает очень важный вопрос теории Солнца — о движении апогея Солнца.

Как известно, Птолемей здесь допустил существенную ошибку: он принял как незыблемый факт, что долгота апогея Μ Солнца навсегда сохраняет одно и то же значение, то самое, которое нашел Гиппарх, а именно: π = 65°30'.

Из текста видно, что аль-Фараби своими наблюдениями подтверждает важное открытие, сделанное арабскими предшественниками об изменении апогея Солнца, что является его большой заслугой в теории Солнца и показывает, что он был не только крупным теоретиком астрономии, но и превосходным практиком-наблюдателем.

При этом аль-Фараби считает, что это открытие принадлежит астрономам мамуновской обсерватории. Есть большие основания полагать одним из его авторов среднеазиатского ученого Халида аль-Мервурриди, участвовавшего в историческом измерении величины Земли в дни халифа аль-Мамун (начало IX в.) и, по свидетельству аль-Бируни, проводившего исследования по измерению долготы апогея. Аль-Бируни, сравнивает наблюдения точек равноденствий и солнцестояния Птолемея, Бану Мусы, аль-Мервурриди, аль-Баттани, Абу-л-Вафы и свои наблюдения. Делает тот же вывод и аль-Фараби: «Из всего, что изложено, ясно, что апогей Солнца перемещается, это противоречит тому, что считал Птолемей» [8, стр. 107—108].

В литературе распространено мнение, по которому факт перемещения апогея Солнца был впервые установлен аль-Баттани (850—929), что не совсем точно.

121. Здесь находится числовая величина наибольшего значения уравнения центра:

122. Имеется в виду доказанная в первой книге теорема синусов для вписанного прямоугольного треугольника.

123. Эта таблица приведена в приложениях к настоящей работе (таблица 6).