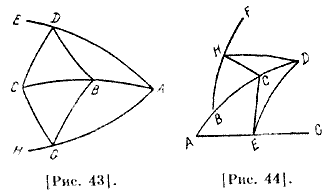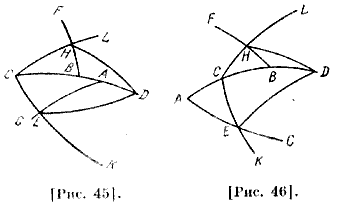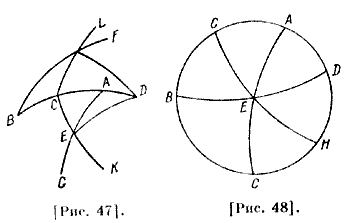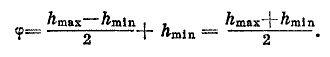Аль-Фараби

КОММЕНТАРИИ К "АЛЬМАГЕСТУ" ПТОЛЕМЕЯ

* Об обитаемых частях Земли и упоминание о целях книги * Об определении азимута восхода * Об определении отношения гномонов к [полуденным] теням во времена равноденствий и солнцестояний * Об особенностях кругов, параллельных небесному экватору * О восхождениях относительно широт * О частных вещах, связанных с определением восхождений * Об определении угла, образуемого пересечением эклиптики и меридиана * Об определении угла, образуемого эклиптикой и горизонтом * Об определении угла, образуемого пересечением эклиптики и круга, проходящего через полюсы горизонта * Примечания *

ВТОРАЯ КНИГА⁶²

«СОКРАЩЕНИЯ АЛЬМАГЕСТА»

Об обитаемых частях Земли и упоминание о целях книги

Он сказал⁶⁴: Земля делится земным экватором, параллельным небесному экватору, и одной из линий, проходящей через два полюса небесного экватора, на четыре части: две южные, две северные четверти; обитаемая часть — приблизительно одна северная четверть. Расстояние от линии зимнего экватора до полюса называется широтой, а то, что от востока до запада — долготой.

Обоснование нашего утверждения о том, что обитаемая часть есть северная четверть, заключается в следующем. Относительно широты мы не нашли никаких обитаемых местностей, для которых при двух равноденствиях тени гномона в середине дня были бы направлены к югу. Я говорю, возможно, кто-нибудь другой после нас найдет то, чего мы не смогли найти⁶⁵. Относительно долготы мы обнаружили, что лунные затмения опережают или запаздывают для всей обитаемой части Земли самое большее на двенадцать часов.

Это общее рассмотрение; в частности, [в этой книге] будет рассматриваться каждая местность в соответствии с ее широтой и нахождением под параллельным небесному экватору кругом, для которого известна высота полюса. Высота полюса определяется с помощью наблюдения предела высоты одной из вечновидимых звезд и предела ее понижения: разделим пополам разности между ними и прибавим ее на предел понижения⁶⁶, или она находится определением градуса небесного экватора с помощью упомянутого инструмента. Она определяется как разность между числом 90 и величиной этого градуса, которая равна высоте полюса⁶⁷.

Кроме того, нужно знать обстоятельства Солнца, то есть когда оно бывает в зените; если бывает, то сколько раз: один или два; отношение [величин] полуденных теней к гномонам в дни солнцестояний и равноденствий; отношение самого короткого дня к равноденственному; состояние видов их разницы; [сюда же относятся] определение восходов [градусов эклиптики], а также определение величины углов, расположенных между дугами больших кругов, и их отношения, которые служат основой в определении возможного наибольшего дня в наклонных климатах по сравнению 19 с экватором. На линии земного экватора дни и ночи не отличаются [по длине] друг от друга, там день и ночь всегда равны.

Теперь определим величину дуги горизонта, расположенной между небесным экватором и косым кругом. Эта дуга называется азимутом восхода⁶⁸.

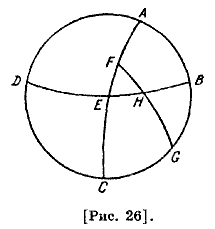
Об определении азимута восхода

Начертим рисунок, соответствующий [параллели, проходящей] через остров Родос, где высота полюса 36 градусов, а наибольший день содержит 14 с половиной [равноденственных] часов. Пусть ABCD — полуденный круг [рис. 26]; половина горизонта — BED, половина небесного экватора — АЕС; южный полюс — G, а Н — [точка] зимнего солнцестояния в квадранте FH, выходящем из полюса G. [Пусть сначала дана величина наибольшего дня] и требуется определить ЕН, которая является азимутом восхода.

Поскольку вращение совершается вокруг полюса небесного экватора G, то F и Η обязательно попадут на полуденный круг АВ в одно и то же время, которое определяется [дугой] FA небесного экватора. Если начинать от середины [неба] под Землей до восхода, то это время определяется обязательно дугой, равной FC. Поэтому продолжительность дня определяется удвоенным временем FA, а продолжительность ночи — удвоенным временем FC, потому что полуденный круг пересекает пополам каждую высокую и низкую дугу. Дуга EF есть половина разности между наибольшим или наименьшим днем и [равноденственным]. Это для данной [параллели] равно одному часу с четвертью.

Поскольку 24 часа соответствуют 360 градусам, то каждый час равняется 15 градусам; следовательно, указанное время будет равно восемнадцати временным градусам и 45 минутам, отсюда полуденное время FA известно.

Следовательно, отношение синуса Ε А к синусу FA составлено из отношения синуса ЕВ к синусу НВ и отношения синуса GH к синусу GF. Отсюда будут известны ВН и НЕ⁶⁹.

Покажем, как по данным величинам дня и дуги горизонта найти высоту полюса, по которой расстояние от горизонта будет известным. Пусть требуется найти BG на том же рисунке, что между полюсом и горизонтом. Поскольку отношение синуса EF к синусу FA составлено из отношения синуса ЕН к синусу НВ и отношения синуса GB к синусу GA и все эти синусы известны, то оставшийся синус GB известен; следовательно, известна дуга GB⁷⁰.

Теперь мы хотим определить разности между наибольшим и наименьшим днем, то есть удвоенную разницу по отношению к равноденственной. Это и есть удвоенная дуга EF, которую следует определить. Поскольку отношение синуса дуги GB к синусу дуги ВА составлено из отношения синуса GH к синусу

HF и из отношения синуса FE к синусу ΕА, то будет известной удвоенная EF на основании того, что мы знаем^7Ι.

Дугу ЕН также можно определить исходя из дуги расстояния полюса, если те остальные будут известными, поскольку отношение синуса GA к синусу АВ составлено из отношения синуса GF, то есть девяносто градусов, к синусу FH, то есть склонения, и из отношения синуса ЕН к синусу ЕВ, которое известно⁷².

Независимо от того, будет ли 20 известное склонение южным или северным, является ли оно полным склонением или склонением градуса, все обстоятельства сохраняются.

Он сказал: отсюда следует, что равные части отрезков [круга эклиптики], т. е. одинаково отстоящие от той же точки солнцеворота, имеют одно и то же склонение, одну и ту же дугу горизонта, одинаковый день и тот же восход. [Вместе с тем доказано], что части, расположенные на одном и том же расстоянии от той же точки равноденствия, имеют с обеих сторон [небесного экватора] одинаковые положения, [то есть образуют равные между собой дуги горизонта и накрест равные друг другу части суток разного наименования]. Это значит, насколько уменьшается продолжительность дня и ночи в одной стороне, настолько увеличивается в другой стороне и наоборот.

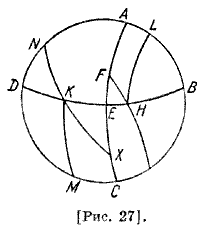
Пусть на том же рисунке точка К описывает круг, параллельный небесному экватору [рис. 27]. Пусть КМ — отрезок этого круга, a HL — отрезок, накрест расположенный к нему. Очевидно, они равны между собой. Предположим, что точка N — северный полюс; проведем через К и N дугу NK, пересекающую небесный экватор в X; тогда СХ будет равна FA, потому что СХ подобна КМ, так как они расположены между двумя дугами, выходящими из полюса небесного экватора. Таким же образом FA подобна HL; следовательно, КМ и HL равны. Так как две подобные дуги, расположенные в одном и том же круге, будут равными, точно так же оставшиеся ЕХ и EF равны. Таким же образом две стороны ХЕ и ХК треугольника ХЕК соответственно равны сторонам FE и FH другого треугольника, углы F и X прямые, следовательно, основание КЕ равно основанию ЕН. Отсюда ясно, что если провести хорды дуг в указанных двух треугольниках, то соответственно будут равными восхождения, азимут восхода, склонения в двух сторонах.

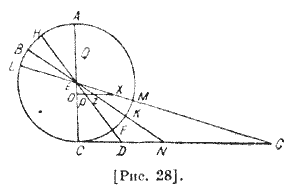
Об определении отношения гномонов к [полуденным] теням во времена равноденствий и солнцестояний⁷³

Около Ε опишем меридиан ABC, АЕС — его диаметр, А — зенит [рис. 28], из С проведем линию, параллельную горизонту. Пусть CG будет [прямой], на которую падает тень, СЕ — гномон⁷⁴. Поскольку Земля мала по сравнению с небесной сферой, то безразлично, будет ли гномон на поверхности Земли или же в самом ее центре. Пусть точка В — точка равноденствия на полуденном круге, тогда ВЕК будет [равноденственным! лучом, a CN — его тенью, пусть

Η — точка летнего солнцестояния, а HEF — его луч, a CD — тень этого луча; L — точка зимнего солнцестояния, LEM — его луч, CG — тень этого луча. Расстояние зенита от небесного экватора равно высоте полюса, угол АЕВ известен; поскольку наибольшее склонение и в северной и в южной сторонах известны, то дуги НВ и BL известны; поэтому будут известными дуга АН и ее угол. Следовательно, дуга АН и ее угол будут известными. Если определены эти дуги 21, то будут известны их центральные углы, их вертикальные углы будут углами треугольников при центре, угол С — прямой, СЕ — 60 частей, поэтому все треугольники известны, потому что треугольник вполне решается по двум углам и стороне, то есть по этим данным находятся остальные. Если точки С и Ε расположить в центре близко друг к другу и принять любую из них центром круга, а другую — концом гномона, то это не повлияет на круг и доказательство будет одно и то же⁷⁵.

Пусть О будет основой гномона, а Ε — его концом; проведем из О перпендикуляр ОХ так, чтобы тень падала на нее; она будет параллельна линии CN; то и другое отношение — одно и то же.

Точно так же, если точку Ε сделаем основой гномона, Q — концом в этом направлении, ЕХ — перпендикуляром, Χ, Ζ, Ρ — концами теней, когда нет различия между углами, которые образуются при Ε и при Q, близкой от нее. По проведенному уже вычислению линия CD, являющаяся тенью при летнем солнцестоянии, будет равна 12,55; линия CN, являющаяся равноденственной тенью, — 48,36, а линия CG — тень при зимнем солнцестоянии — 103,20. Тем самым уже доказано, что если известны высота полюса и склонение, то можно легко определить отношение теней и гномона.

Отсюда легко узнать высоту [полюса] и склонение по данному отношению теней и гномона, так как можно определить эти дуги по углам указанного треугольника. Однако надежным путем определения наибольшего склонения и высоты полюса является [приведенный выше] первый способ, потому что полуденная тень неизвестна ввиду непрерывности перехода теней от убывания к увеличению и от увеличения к убыванию и поэтому трудно наглядно отмечать время равноденствия, а также тени во время зимнего солнцестояния трудно различимы.

Об особенностях кругов, параллельных небесному экватору⁷⁶

Птолемей нарисовал круги, параллельные небесному экватору и проходящие через зенит местности, находящейся под ними. Он взял расстояния между этими [параллелями] через каждую четверть часа. На земном экваторе ночь и день всегда равны. Если направимся в сторону полюса, наблюдается разность [между ними]. Чем ближе к полюсу, тем больше эта разность. Он выбрал [параллели], о которых будет идти речь, через каждую четверть часа.

Он сказал: что касается земного экватора, то он служит границей [между] нашей обитаемой и необитаемой пустой южной частью. Поскольку сфера [у экватора] прямая, то горизонт делит пополам все круги, параллельные небес ному экватору, поэтому там день и ночь всегда равны. Что касается других мест, то один только небесный экватор делится пополам кругом горизонта, а остальные круги делятся на неравные части. Для каждого круга, который ближе к полюсу, примыкающему к обитаемой местности, верхние отрезки параллели больше нижних, поэтому день длиннее ночи. Кругу земного экватора свойственно, что тень направляется иногда к югу, когда Солнце проходит на север от него, а иногда — к северу, когда Солнце проходит к югу от него. Предел длины и роста тени у [экватора] бывает в полдень во время солнцестояния. Это будут двадцать шесть с половиной частей гномона из шестидесяти частей. Для его жителей все звезды будут восходящими и заходящими, среди них не будет ни вечно невидимых, ни вечно видимых.

Он сказал: что касается того, есть ли жители там или нет, то по этому погоду говорят, что, 22 возможно, есть, тате как в том месте [все времена года] должны быть предельно умеренны. Там Солнце не задерживается долго в зените, а быстро смещается, поэтому лето бывает умеренным. Оно не удаляется сильно от зенита при солнцестоянии, поэтому зима будет умеренной. В частности, мы говорили много по этому поводу; это можно найти в моих книгах по физике.

Что касается того, какие страны и какие местности там, то, когда Птолемей писал «Альмагест», он не знал об этом и сказал: то, что говорят об этом, является предположением. Позднее он узнал о некоторых и включил их⁷⁷ в [свою] книгу «География»⁷⁸.

Что касается других параллелей, где есть обитаемые местности и высота полюса в каждой из них равна широте [данной параллели], то для них имеются вечно видимые звезды, они описывают круги, среди которых наибольший с полудиаметром, равным широте [с центром в этом полюсе], касается горизонта, но эти звезды — вечно невидимые с другого полюса.

После линии земного экватора есть второй круг, параллельный линии экватора. Для него наибольший день — 12 с четвертью часов; его широта 4; 15 градуса. Эта параллель проходит через остров Тапробани. Поскольку широта меньше [наибольшего] склонения, то она будет иметь двусторонние тени, так как Солнце два раза находится в зените ; тогда не бывает тени. Когда его расстояние от точки летнего солнцестояния в обеих сторонах будет равно 79; 30 градусам, равноденственная тень будет иметь 4;25 частей из шестидесяти; летняя тень 21; 20, а зимняя — 32.

У следующей параллели наибольший день равняется 12;30 [часам], широта—8;25, градусам; он проходит через Авалийский залив; имеет двусторонние тени; Солнце здесь два раза будет в зените, когда оно отстоит от точки [летнего] солнцестояния в обеих сторонах на расстоянии 69 градусов; равноденственная тень будет иметь 8; 50 частей, летняя тень — 16; 35, зимняя — 37; 54 частей.

Четвертая [параллель] имеет наибольший день — 12 и три четверти [часов], широту— 12; 30 градусов и проходит через Адуллийский залив, она имеет двусторонние тени, так как Солнце дважды бывает в зените; равноденственная тень будет иметь 18; 20 частей, летняя — 12, а зимняя 44; 40.

Наибольший день пятой [параллели] — 13 часов, широта— 16; 27 градусов. Проходит она через остров Мероэ; имеет двусторонние тени, так как Солнце дважды бывает в зените, [когда оно отстоит от точки летнего солнцестояния] на расстоянии 45 градусов; равноденственная тень равна 17; 45 частям, летняя — 7; 45, а зимняя — 51.

У шестой [параллели] наибольший день 13 с четвертью часов, широта 20; 14 градусов. Она проходит через Напату, имеет двусторонние тени, так как Солнце дважды бывает в зените, [когда отстоит от точки летнего солнцестояния] на расстоянии 31 градус, равноденственная тень равна 22;10 частям, летняя — 3; 45, а зимняя — 38; 10.

Седьмая [параллель] имеет наибольший день 13 с половиной часов, широту — 23; 51 градус и проходит через Сиену, у которой широта равна [наибольшему] склонению, поэтому она имеет только северные тени, так как Солнце только один раз бывает в зените при точке солнцестояний; равноденственная тень равна 26; 30 частям, зимняя — 65; 50, а летняя будет без тени, и на тех параллелях, которые севернее этой, будет иметь только одну тень; Солнце никогда не бывает в зените.

На восьмой [параллели] наибольший день 13 и три четверти часа, широта 27;12 градусов. Она проходит через Птоламиду; равноденственная тень равна 36; 50 частям, зимняя — 74; 10, летняя — 3; 30.

У девятой [параллели] наибольший день 14 часов, широта 30; 22 градуса. Проходит через страны Нижнего Египта; летняя тень равна 6;50 частям; равноденственная — 35; 05, зимняя — 83;05.

Наибольший день десятой [параллели] 14 с четвертью часов, широта 33, 18 градусов. Проходит через середину 23 Сирии, летняя тень равна 10 частям, равноденственная тень — 39; 30, а зимняя — 93; 05.

Одиннадцатая [параллель] имеет наибольший день 14,30 часов, широту — 36 градусов и проходит через Родос, летняя тень равна 12,55 частям, равноденственная — 47; 50, зимняя — 103;20.

У двенадцатой [параллели] наибольший день 14,45 часов, широта 38; 35 градусов. Она проходит через Смирну; летняя тень равна 15; 40 частям, равноденственная — 48; 36, а зимняя — 114; 55.

Наибольший день тринадцатой [параллели] 15 часов, широта 40; 56 градусов. Она проходит через страну Сехитуос (Геллеспант), летняя тень равна 18; 30 частям, равноденственная 52; 10, а зимняя — 127 ; 50.

Четырнадцатая [параллель] имеет наибольший день 15,15 часов, широту — 43; 15 и проходит через Массилию, летняя тень равна 20; 50 частям, равноденственная— 55; 55, а зимняя — 144.

У пятнадцатой [параллели] наибольший день 15,30 часов, широта — 45; 10 градусов. Она проходит через середину Понта; летняя тень равна 23;15 частям, равноденственная — 60 и соответствует частям гномона, а зимняя — 155.

Наибольший день шестнадцатой [параллели] 15,45 часов, широта — 46; 51 градусов и проходит через реку Истру; летняя тень равна 25; 30 частям, равноденственная — 63; 55, а зимняя — 171; 30.

Семнадцатая [параллель] имеет наибольший день 16 часов, широту — 48; 32 и проходит через устье реки Борисфени; летняя тень равна 27; 30 частям, равноденственная — 67; 60, а зимняя — 188;35.

У восемнадцатой [параллели] наибольший день 16,15 часов, широта 50; 15 градусов. Параллель проходит через середину Меотидского озера (моря); летняя тень равна 29;55 частям, равноденственная — 71; 40, а зимняя — 208; 20.

Наибольший день девятнадцатой [параллели] 16,30 часов, широта — 51; 40 градусов, проходит она по югу Британии; летняя тень равна 31; 25 частям, равноденственная — 75; 25, а зимняя — 229; 30.

Двадцатая [параллель] имеет наибольший день 16,45 часов, широту — 52; 50 градусов и проходит через устье Рейна; летняя тень равна 33;20 частям, равноденственная — 79; 05, а зимняя — 253; 10.

У двадцать первой [параллели] наибольший день 17 часов, широта — 54; 30 градусов. Проходит она через устье Ганайс; летняя тень равна 34;55 частям, равноденственная — 82; 35, а зимняя — 278; 45.

Наибольший день двадцать второй параллели — 17,15 часов, широта — 55 градусов. Она проходит через [юг] страны Великой Британии; летняя тень равна 36;15 частям, равноденственная — 85,40, а зимняя — 304; 30.

Двадцать третья [параллель] имеет наибольший день 17,30 часов, широту 56 градусов и проходит через середину страны Великой Британии; летняя тень равна 37;40 частям, равноденственная — 88; 50, а зимняя — 335; 15.

У двадцать четвертой [параллели] наибольший день 17, 45 часов, широта — 57 градусов. Проходит через местность, называемую Катурактонией, в стране Британии; летняя тень равна 39; 20 частям, равноденственная — 92; 25, а зимняя — 372; 05.

Наибольший день двадцать пятой [параллели] 18 часов, широта — 58 градусов. Она проходит через юг Малой Британии, летняя тень равна 40; 40 частям, равноденственная — 96, а зимняя—449; 50.

Двадцать шестая [параллель] имеет наибольший день 18,30 часов, широту — 59; 30 градусов и проходит через середину Малой Британии.

Он сказал: теперь уже мы не пользуемся приращением в одну четверть часа, потому что дальние круги близко прилегают друг к другу по расстоянию. Мы говорим: параллель, для которой наибольший день будет 19 часов, а широта — 61 градус, проходит через крайний север Британии, а параллель, для которой наибольший день 19, 30 часов, а широта 62 градуса, проходит через Эбудские острова; [параллель], для которой наибольший день 20 часок, а широта 63 градуса, проходит через остров Фулу; [параллель], для которой наибольший день 21 час, а широта 04;30 градусов, проходит через неизвестные племена [славян⁷⁹]. На параллели 24, где наибольший день 22 часа, широта 65; 30 градусов; [на параллели], где наибольший день 23 часа, широта 66 градусов; [параллель], для которой наибольший день 24 часа, а широта 66; 30 градусов является круготеневой, так как Солнце там не заходит только в день летнего солнцестояния и тени гномонов вращаются по кругу. Здесь круг летнего солнцестояния будет вечно видимым, а круг зимнего солнцестояния — вечно невидимым, так как они будут накрест противоположно касаться круга [горизонта] земли, потому что параллель описанной вершиной Рака касается горизонта.

Если полюс эклиптики будет вращаться вокруг полюса небесного экватора, то полюс эклиптики будет к югу от полюса экватора. Когда широта является полным склонением, то полюс эклиптики должен быть в зените и совпадает с полюсом горизонта; поэтому круг эклиптики совпадает с кругом [горизонта] Земли. Тогда [тропик] Рака будет спускаться впил до тех пор, пока он не коснется горизонта с севера, а [тропик] Козерога будет подниматься и верх до тех пор, пока он не коснется горизонта с противоположной южной [стороны]. Если восходит тонка весеннего [равноденствия], то круг эклиптики является горизонтом, так как в это время полюс эклиптики находится в зените, а полюс небесного экватора будет к северу от него. Поэтому Рак неизбежно будет на горизонте и на меридиане, а Овен — на Востоке. Если кто-нибудь захочет добавить [что-либо] к этому, он сможет сделать это из предпосланных принципов⁸⁰.

Отсюда ясно, что там, где высота полюса приблизительно равна 67 градусам, [Солнце] совсем не заходит на протяжении половины знака Зодиака с обеих сторон Рака, т. е. от точки [летнего] солнцестояния; здесь наибольший день будет продолжаться приблизительно целый месяц; там, где высота полюса будет 69; 30 градусов, [Солнце] не заходит на протяжении одного знака Зодиака, и наибольший день будет продолжаться приблизительно два месяца; там, где высота полюса 73; 20 градусов, [Солнце] не заходит на протяжении полутора знаков Зодиака, расположенных между двумя созвездиями — Тельцем и Львом, и наибольший день будет продолжаться приблизительно три месяца. Там, где высота полюса 78; 20 градусов, [Солнце] не заходит на протяжении двух знаков Зодиака в каждую из двух сторон, и наибольший день будет продолжаться приблизительно четыре месяца; там, где высота полюса 84 градуса, оно не заходит на протяжении двух с половиной знаков Зодиака в каждую из двух сторон, и наибольший день будет продолжаться пять месяцев. Там, где высота полюса 90 градусов, [Солнце] не заходит на протяжении трех знаков Зодиака в каждую сторону, и наибольший день будет продолжаться шесть месяцев. При этом южная половина шесть месяцев не восходит, а северная половина шесть месяцев не заходит. Таким образом, шесть месяцев будет день, а шесть месяцев — ночь. Здесь круг небесного экватора есть круг горизонта, являющегося большим кругом обеих частей небосвода: вечно видимой и вечно невидимой и общей границей между ними.

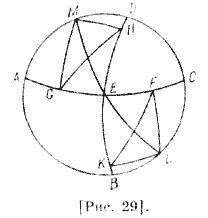
О восхождениях относительно широт⁸¹

Мы уже говорили о восхождениях в прямой сфере. Теперь будем говорить о восхождениях в наклонной сфере.

Мы утверждаем, что дуги [эклиптики], равноотстоящие от южной и северной точек равноденствия в отношении широт, имеют одинаковые восхождения.

Пусть ABCD — меридиан [рис.29], BED — круг горизонта, АЕС — небесный экватор, G — точка весеннего равноденствия, GH — дуга северного наклонного круга; пусть F — та же самая точка, ее соединим с другой и получим дугу южного наклонного круга KF, равную GH, их восхождения FE и EG. Мы утверждаем, что они равны.

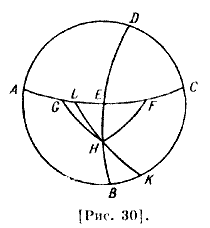
Представим полюс, соответствующий точке G, находящийся в L; с другой стороны пусть это будет точка М. Проведем через эти полюсы отрезок круга LEM и дуги FL, LK, GM и МH больших [кругов]. Дуга GH по данному 25 равна дуге KF, дуга LK равна дуге МH, потому что два треугольника равны. Поэтому дуги ЕК и ЕН, являющиеся азимутами восхода, равны, дуги ME и EL равны как расстояние от полюса до точки [небесного экватора]. Следовательно, стороны треугольника ЕНМ такие же, как соответственные стороны треугольника ELK. Следовательно, угол ELK равен углу ЕМН, но угол KLF равен углу HMG, так как они стягиваются равными дугами. Две стороны равны соответствующим сторонам другого, углы FLE и EMG равны. Тогда основание EF равно основанию EG.

Мы утверждаем, что если восхождения каждой из двух равных дуг наклонного [круга] находятся на двух сторонах одной точки солнцестояния, тогда то, что между одной из них и точкой солнцестояния, равно тому, что между другой и той же точкой солнцестояния. Например, [восхождения] двух знаков Зодиака — Овна и Девы. Если сложить их, они будут равны сумме восхождений соответствующих двух дуг на линии экватора.

Пусть ABCD — меридиан [рис. 30], BDE — половина горизонта и АСЕ — половина небесного экватора; GH — южная дуга, расстояние которой от зимнего солнцестояния равно расстоянию дуги FH, G — осенняя, a F — весенняя точка, Η будет общей точкой круга горизонта и этих двух дуг, потому что эти дуги лежат внутри одного и того же круга, параллельного небесному экватору.

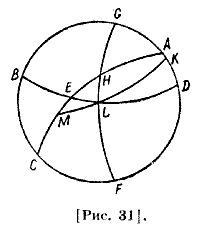
Проведем через Η и полюс небесного экватора четверть большого круга, которая будет в прямой сфере равнозначна горизонту. Это — KHL. Поскольку FE — восхождение FH, EG — восхождение HG, то сумма FG есть восхождение двух дуг в этом [климате]. Но FL — восхождение FH на прямой сфере и GL — восхождение HG на прямой сфере; их сумма равна FG, это сумма восхождений не в прямой сфере⁸². Отсюда мы выяснили, если определим восхождения только для одной четверти, то этого достаточно для определения его и для других [четвертей].

Вычислим это для острова Родос, о котором мы выше упомянули. И пусть ABCD—меридиан [рис. 31], BED— круг горизонта, АЕС — половина круга небесного экватора, GHF — половина круга эклиптики, Η — точка весеннего равноденствия; DK — высота полюса, К — точка полюса; через нее проведем четверть круга, проходящего также через пересечение наклонного круга и горизонта, то есть через точку L до точки М. Пусть, например, LH будет один знак Зодиака, соответствующий Овну. Требуется найти величину ЕН.

Доказано, что отношение синуса KD к синусу DC составлено из отношения синуса KL к синусу LM и из отношения [синуса] ЕМ к [синусу] ЕС; но DK — это высота полюса 26, DC — остаток после отнятия известной дуги KD от известной дуги КС; KL известна, так как она расстояние начала Тельца от полюса небесного экватора, которое есть дополнение его склонения; ЕС известна, будет известна и ME; HM — восхождение Η в прямой сфере, которое известно; отсюда НЕ известна. По вычислению восхождение Овна, которое соответствует острову Родоса, будет равно 19; 12 градусам. Отсюда следует, что и Рыба имеет такое же восхождение; Весы дополняют восхождение Рыбы в прямой сфере, а Дева — восхождение Овна.

Если линия HL содержит сумму [двух знаков Зодиака], соответствующих Овну и Тельцу, то, поскольку мы знаем восхождение одного Овна, будем знать восхождение другого. Для восхождения Тельца остается 22;46 градусов. Точно так же определяется [восхождение] Водолея через [восхождение] Рыбы, Льва — через Девы, Скорпиона — через Весы.

Поскольку для данной широты, то есть для острова Родос, известны наибольший и наименьший дни, то ясно, что одна часть от Рака до Стрельца соответствует 217; 30 временным [градусам], другая — 142; 30. Таким образом, две четверти, прилегающие к точке весеннего равноденствия, будут с известными восхождениями. Каждая из них восходит вместе с 71; 15 [временными градусами]. Из этого видно, сколько остается для каждого из Тельца и Козерога. Оно будет составлять 29;17 градусов, а каждое из созвездий Рака и Тельца — 36;15 градусов. Это правило дает возможность определить восхождения и для более мелких делений, чем полного знака Зодиака. Птолемей упомянул, что для этого есть другой более легкий и удобный способ.

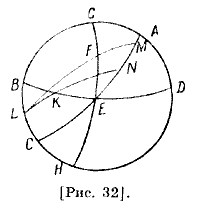
Он сказал: пусть ABCD — меридиан [рис. 32], АЕС — половина круга небесного экватора, GH — половина эклиптики, пусть Ε совпадает с точкой весеннего равноденствия на пересечении горизонта BED. Проведем известную дугу EF и построим дугу FK, пересекающую горизонт и параллельную небесному экватору. Пусть южный полюс небесного экватора — точка L; построим четверти кругов LFM и LKN; известно, что ЕМ — восхождение EF на экваторе, поскольку в потенции горизонт для тех же самых есть линия FM. В этой местности восхождения равны дуге MN из-за того, что FK параллельна MN и подобна ей, так как их отсекли две подобные дуги, [проведенные] из полюса. А подобные же дуги восходят вместе. Но FK — это та [дуга], на которой вращался параллельный круг с того времени, когда F до Ε была на горизонте. Тогда ΕΝ — избыток восхождений экватора над восхождением этой широты. На этом рисунке можно ошибиться и думать, что когда точка F находится на горизонте, точка Μ также находится на горизонте, и они восходят вместе, то есть EF и ЕМ [равны], а это не так. Это бывает на горизонте экватора. Здесь же на горизонте BED вместе с F имеется другая точка, расстояние которой до Ε [равно] расстоянию от Μ до N.

Мы сделаем рисунок более простой, чем этот.

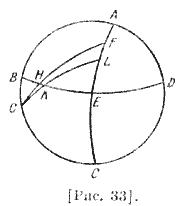
Пусть ABC — меридиан 27 для места, широта которого известна [рис. 33], AЕС из круга небесного экватора, BED — половина горизонта, G — южный полюс, H — общая точка [горизонта] и [параллели] зимнего солнцестояния, проведем GH до F, т. е. до четверти круга, К — общая точка [горизонта] и [параллели] градуса [эклиптики]; проведем GKL. Тогда отношение синуса дуги FH к синусу HG составлено из отношения синуса FE к синусу EL и из отношения синуса LK к синусу KG. Что касается синуса FH, то он известен, так как он — синус полного склонения, и поэтому синус HG известен; синус LK известен как склонение градуса эклиптики; синус KG известен как дополнение склонения; синус FE известен как половина разности между наибольшим и наименьшим днями; они известны нам для данной широты, равной высоте полюса. Мы доказали, что это можно узнать, если определить высоту полюса. Тогда оставшийся синус LE известен; LE — разность между восхождением по широте и восхождением в прямой [сфере]. А восхождение в прямой [сфере] известно⁸³.

Птолемей далее составил⁸⁴ таблицу, поместив в первый столбец знаки Зодиака, во второй — десятки градусов, так как различие меньше этого не существенно ; в третий — временные градусы и минуты; в четвертый — сложенные [времена], начиная от Овна как начала квадранта⁸⁵.

Из всего изложенного выше ясно, что если ты вычислишь [восхождение] для одного квадранта, то этого достаточно [для остальных].

О частных вещах, связанных с определением восхождений⁸⁶

Из того, что можно определить через восхождение, в первую очередь следует отметить нахождение величины дня и ночи по данному градусу Солнца. Что касается дня, то посчитаем времена дуги дня в отношении местностей от градуса [эклиптики], занимаемого Солнцем, до противоположного ему градуса; что касается ночи, то поступаем в обратном порядке. Тогда пятнадцатая часть этого будет число равноденственных часов. Если эту сумму разделим на двенадцать, то получим время косого часа⁸⁷.

Другой, более легкий способ. Возьмем шестую часть разности сложенных времен в таблице восхождений градуса [эклиптики], занимаемого Солнцем для дня, или градуса противоположного этому для ночи, прибавим ее к пятнадцати временным северным градусам⁸⁸ и отнимем ее из южных [градусов], т. е. вычтем сложенные времена для круга, параллельного небесному кругу, от сложенных времен для круга, параллельного данному климату, потому что эта разность соответствует четверти круга, которая приходится на долю шести часов; отсюда будет известен косой час.

Далее, умножив [количество] косых часов на [число] временных градусов этого дня или ночи после деления на пятнадцать, получим [количество] равных часов⁸⁹. Можно превратить ровные [часы] в косые.

Если будет известен косой час, то отсюда вычислим восхождение. Для этого умножим его на [число] часов, прошедших от восхода или захода Солнца, и затем это число отсчитаем от градуса, [занимаемого] Солнцем (днем), или противоположного градуса (ночи), в соответствии с восхождением широты [местности] в последовательности [знаков] Зодиака и получим восхождение.

Если мы хотим [определить] градус середины неба, то умножим [число] косых часов от полудня прошедшего дня на соответствующее одному часу число временных [градусов]; затем полученное число отсчитаем от градуса в последовательности знаков Зодиака по восхождениям в прямой сфере. Тот градус, на который достигло это число, и есть середина неба над Землей.

Если известно 28 восхождение и нужно найти середину неба над землей, то возьмем сумму чисел из составленной [таблицы], соответствующую восхождению, и из нее вычтем девяносто временных [градусов] и получим то, что соответствует временному [градусу] в [таблице] для прямой сферы. Следовательно, будет известна середина неба. [Наоборот], если прибавим к тому, что [соответствует градусу середины неба в таблице], девяносто часовых [градусов], то получим соответствующее восхождение страны.

Ясно, что для живущих под одним и тем же меридианом Солнце будет отстоять от полудня или полуночи на одинаковое [число] равных часов, для тех же, кто живет на разных меридианах, оно будет различно, при этом опережает или отстает на [разность, выраженную во временных градусах] небесного экватора, которая по величине равна [разности] градусов между этими меридианами.

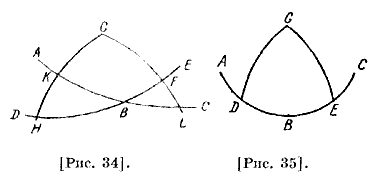
Об определении угла, образуемого пересечением эклиптики и меридиана

Изложим обстоятельства, относящиеся к углу, расположенному между эклиптикой и меридианом.

Он сказал, что прямой угол на сфере есть угол, стягиваемый четвертью большого круга, полюсом которого служит [вершина] указанного угла. Отношение этого угла к четырем [прямым] углам, образуемым пересечением дуг больших кругов, есть отношение этой дуги к кругу, который представляет собой четырежды взятую указанную дугу. Эта дуга стягивает девяносто градусов, а искомый угол получается как часть этого.

Здесь мы хотим определить величины углов, образуемых пересечениями косого круга и меридиана, косого круга и горизонта и косого круга и круга, проходящего через зенит к данной части (точки). Определение этих углов очень полезно, особенно необходимо для нахождения параллакса⁹⁰ Луны.

Он сказал: пусть мы будем говорить о восточно-северном угле из четырех образуемых углов. Для простоты начнем прежде всего с угла, образуемого косым кругом и меридианом. Сначала докажем, что каждые две данные [точки], одинаково отстоящие от точки равноденствия, образуют два равных упомянутых угла. Пусть ABC — [дуга круга] небесного экватора [рис. 34], DBE — из косого круга, G — полюс небесного экватора, В — точка равноденствия, и пусть ВН и BF равны, дуги КН и FL — из меридиана. Поскольку треугольники КНВ и BFL имеют [попарно] равные стороны, то на основании того, что мы знаем, они подобные. Следовательно, угол Η равен соответствующему углу BFL, то есть углу GFE, в силу их вертикальности.

Пусть ABC — из эклиптики, В — точка солнцестояния [рис. 35]. Мы утверждаем, что если две дуги, равноотстоящие от этой точки, например BE, ED, и образуют с меридианом два угла, расположенных в одну и ту же сторону, например восточную, то эти углы равны двум прямым. Эти углы — GDB и GEC.

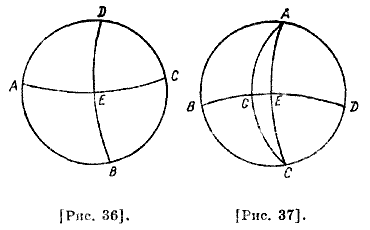
Действительно, угол GEC вместе с углом GEB равен двум прямым, углы GEB и GDB равны, как стягиваемые равными дугами GD и GE. 29 Это потому, что [расстояния] от полюса до двух точек [эклиптики], равноотстоящих от точки солнцестояния, одинаковы, то есть склонения одинаковы.

А также докажем, что два угла солнцестояний между меридианом и [эклиптикой] прямые.

Пусть ABCD — меридиан [рис. 36], АЕС — половина косого круга, А — точка зимнего солнцестояния. Сделаем А полюсом и из него на расстоянии, равном стороне квадрата, [вписанного в большой круг], опишем круг DEB⁹¹. Дуга DE будет равна четверти круга, так как меридиан ABCD проходит через полюс DEB и полюс эклиптики. Следовательно, [угол] DAE прямой. Точно так же определим угол у [точки] летнего [солнцестояния].

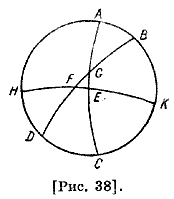
Пусть подобно этому ABCD будет меридианом [рис. 37], АЕС — половина круга небесного экватора, AGC — половина эклиптики, А — точка осеннего равноденствия. Через [точку А] как из полюса опишем полукруг BGED. Поскольку круг ABCD проходит через полюсы круга АЕС, каждая из AG и ED составляет четверть круга, таким образом, G будет точкой зимнего солнцестояния, a GE — известна; следовательно, вся GD будет известна; стягиваемые ею угол GAD и оставшийся GCD будут известны.

Пусть на этом рисунке BGD — полукруг эклиптики [рис. 38], BG— [дуга, соответствующая] Деве, G — точка осеннего равноденствия и AGEC— полукруг небесного экватора. Из полюса В опишем половину большего круга KEFH.

Каждая из дуг ВН, BF и ЕН обязательно окажется равной четверти круга. Тогда отношение синуса ВА к синусу АН, которое известно, составлено из отношения синуса BG к синусу GF и из отношения синуса EF к синусу EH. BG — [дуга, соответствующая] Деве, известна, GF как дополнение ВС известна, ЕН — четверть круга — известна; итак, искомая EF известна. Поскольку ЕК известна, то вся KEF известна; следовательно, искомый угол KBF известен. Поэтому угол Скорпиона будет известным, а каждый из углов, остающийся от двух прямых, — тоже известен.

Если GB принимает другое значение, то мы определим угол, а также противоположный ему угол с другой стороны этой точки и со стороны точки солнцестояния. Так определяются все углы.

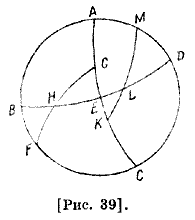
Об определении угла, образуемого эклиптикой и горизонтом.

Что касается угла, образуемого косым кругом и горизонтом в прямой сфере, то можно показать, что он равен углу, образованному наклонным кругом и меридианом. А что касается того, что на наклонной сфере, то мы утверждаем, что угол, образуемый горизонтом и дугой из наклонного круга, измеряемой от точки равноденствия, и [угол], образуемый горизонтом и дугой, восхождение которой равно восхождению этой дуги и находящейся на том же расстоянии от той же точки, равны. Эта дуга находится под землей.

Пусть ABCD 30 — меридиан [рис. 39], АЕС — небесный экватор, BED — горизонт, MLK — наклонная дуга над землей, HF — другая, равная ей дуга под землей, G — точка осеннего равноденствия (восходящая), а К — та же самая точка под землей. Мы утверждаем, что углы EHG и ELK равны, потому что по доказанному треугольники ELK и EGH — с равными сторонами и углами. Дуги ЕК и EG равны по построению. Следовательно, эти углы будут равными.

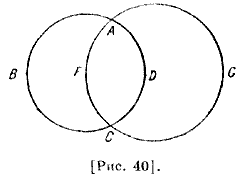
Два [диаметрально] противоположных [угла], образуемые наклонным кругом и горизонтом, то есть восточный и западный углы, вместе равны двум прямым.

Пусть ABCD — круг горизонта, АЕС — наклонный круг, они пересекаются в А и С [рис. 40]. Поскольку углы EAD и BAG, взятые вместе, равны двум прямым и угол GCD равен углу GAD, то углы DAE и DCG [вместе] равны двум прямым.

Так как два угла при точках, равноотстоящих от точки равноденствия и горизонта, одинаковые, то их восхождения и захождения одни и те же. Поэтому восточные и западные углы при двух точках, равноотстоящих от одной и той же точки солнцестояния, вместе равны двум прямым. Эти углы — восточно-северный со стороны востока и западно-северный со стороны запада.

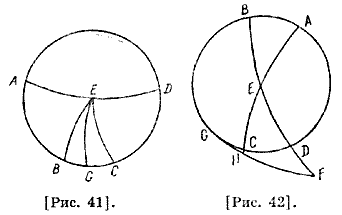
Если определим восточный, то [тем самым] определим и западный [угол], так как это остаток от двух прямых. Чтобы показать, как это делается, мы обратимся к первому рисунку [34]. Если точки Я и L находятся на одном и том же расстоянии от точки солнцестояния, то угол GHE равен углу ELK; следовательно, западный угол DBK вместе с СВЕ равен двум прямым, так как он вместе с ELK равен двум прямым.

Нарисуем параллель, где высота полюса 36 градусов, ABCD — меридиан [рис. 41], AED — восточный полукруг горизонта, EG — четверть небесного экватора, ЕВ — четверть наклонного круга, Ε — точка осеннего равноденствия, а ЕС — четверть наклонного круга, у которой Ε — точка весеннего равноденствия, С — точка зимнего, а В — летнего солнцестояния.

Дуга DG — известна, так как она представляет собой величину, которая остается после вычитания [от прямого угла] высоты полюса; CG и BG известны как наибольшие склонения ; СВ и BG известны; Ε — полюс полуденного круга. Таким образом, каждый из углов, образуемых при Е, будет известен; будут известны углы у начала Весов и Овна.

Предположим, что требуется определить, например, восходящий угол Тельца. Пусть ABCD — меридиан [рис. 42], a BED — восточная половина горизонта, АЕС — половина эклиптики, Ε — начало Тельца 31.

Мы уже показали, что для этого климата восходу начала Тельца соответствует земной столб⁹² — 17; 41 градусов Рака; тогда дуга ЕС будет меньше четверти окружности. Из полюса Ε на расстоянии, равном стороне квадрата, то есть EG, построим дугу [круга] FHG и дополним четверти круга ЕСН и [EDF]. Тогда дуги DCG и FHG будут равняться двум четвертям [круга], так как горизонт BEF проходит через полюсы GCD, GHF. Это потому, что Ε — полюс GHF, затем круг горизонта проходит через полюс меридиана, как и меридиан обязательно проходит через полюс горизонта. Следовательно, полюс GCD находится на горизонте BED.

Расстояние С от небесного экватора известно; расстояние небесного экватора от точки G, то есть от нижнего зенита, известно, тогда их сумма, то есть CG, известна; оставшаяся дуга, то есть CD, известна. Точка Н, находящаяся от Ε на [расстоянии] девяносто градусов, известна, и ее расстояние от небесного экватора известно; расстояние небесного экватора от G известно, так как высота полюса известна. G — полюс горизонта с нижней стороны. Дуги GH и HF известны.

Отношение синуса ED к синусу DF составлено из отношения синуса ЕС к синусу СН и из отношения синуса GH к синусу GF. Но дуга ED — то, что остается от четверти круга после вычитания азимута восхода, это — дуга горизонта до начала Тельца для данной местности, DF — дополнение до девяноста градусов; ЕС, СН и GF — известны. Отсюда становятся известны GH и HF. Следовательно, будет известен угол CED.

Об определении угла, образуемого пересечением эклиптики и круга, проходящего через полюсы горизонта.

Из величины этих углов будут определены и величины соответствующих дуг, заключенных между [эклиптикой и] кругом, проходящим через полюсы горизонта, то есть то, что между зенитом и сечением этого круга с наклонным кругом. Мы утверждаем, что каждая из дуг, отстоящая от одной и той же точки солнцестояния, отсекает [по обеим сторонам меридиана] одинаковые временные [углы], и два угла, взятые с ними в одной стороне, равные двум прямым, и две дуги, проходящие через зенит и [концы] этих дуг, будут равными.

Пусть ABC — дуга меридиана [рис. 43], В — точка зенита, С — полюс небесного экватора; проведем ADE и AGH из одной и той же точки А солнцестояния так, чтобы G и D находились на равных расстояниях от нее. Из полюса С к временным [точкам], то есть к концам одинаковых AG и AD, проведем дуги CG и CD, а также дуги BD и BG от зенита В. Поскольку AG и AD равны и углы при С равны, стороны GC и ВС равны сторонам DC и СВ, основания DB и BG равны между собой, соответствующие углы тоже равны. По уже доказанному, углы CDE и CGA [вместе] равны двум прямым. Но BDC равен CGB и, следовательно, BGC и BDE [вместе] равны двум прямым. Это то, что мы хотели доказать.

У каждой из точек эклиптики, отстоящей к востоку 32 и западу от меридиана на одинаковые временные [углы], будут равны дуги больших кругов, проведенных через зенит и эти точки, а сумма углов восточной и западной дуг равна удвоенному углу, образуемому при точке на меридиане, если обе полученные точки будут находиться или севернее, или южнее зенита. Допустим, что [эти точки] расположены южнее.

Пусть ABCD — дуга меридиана [рис. 44], С — зенит, D — полюс небесного экватора, АЕ, BHF — дуги наклонного круга, расположенные так, что точки Ε и Η — одна и та же точка (восточная и западная). Проведем через них и зенит, [а также] полюс дуги СЕ, СH, DH. Как и раньше, доказывается, что треугольники DHC и DEC имеют равные стороны и углы, поэтому равны углы при D, равны между собой DE и DH; следовательно, равны их основания — дуги, [проходящие] через зенит, то есть СЕ и СН.

Я утверждаю, что углы CEG и СНВ [вместе] равны удвоенному DE, взятому при меридиане. Поскольку углы DEG и DHB, которые получаются от пересечения эклиптики с меридианом в одной и той же точке, равны, а угол DEC равен углу DHC, то, следовательно, углы DEC и СНВ [вместе] равны углу DEG; таким образом, если прибавить их к углу DEG, то CEG и СНВ [вместе] будут равны удвоенному DEG.

Пусть эти две точки А и В расположатся севернее точки С [рис. 45]. Поскольку DEG есть DHB, a DEK — DHL, то углы DEC и DHC равны как соответственные, поэтому угол DEK равен DHL, и, следовательно, весь [угол] LHB равен сумме [углов] DEG и DEK; если прибавить LHB к KEG, остающегося от DEG [при взятии DEK], то эта сумма будет равна удвоенному углу DEG.

В подобном же рисунке положим, что одна из точек, то есть восточная от середины неба точка А, расположена к югу от зенита, а точка В — севернее от него. Я утверждаю, что вместе взятые углы CEG и LHB будут на два прямых больше удвоенного угла DEG [рис. 46].

Поскольку угол DEC равен углу DHC, в силу равенства сторон двух треугольников, то угол DEC вместе с DHL равен двум прямым. Но угол DEG есть DHB, потому что эти углы, как мы уже упомянули, образованы пересечением дуг, проходящих через полюс и данную точку эклиптики в обеих сторонах; тогда, если сложить [сумму] DEG и DEC [с суммой] DHB и DHL, получится удвоенный DEG, то есть DEG и DHB [вместе], и сумма DEC и DHL, которая равна двум прямым. Таким образом, эта сумма равна удвоенному DEC и двум прямым. Следовательно, CEG и LHB [вместе] будут больше удвоенного 33 DEG, т. е. DEG и DHB [вместе], на двух прямых, то есть на DEC и LHD [вместе].

Если предположим, что точка А северней, a S — южней от зенита [рис. 47], то углы KEG и СНВ вместе меньше удвоенного DEG, который равен DEG и DHB вместе. Избыток удвоенного DEG над KEG и СНВ вместе есть CHD и DEK [вместе], которые, как мы знаем, равны двум прямым.

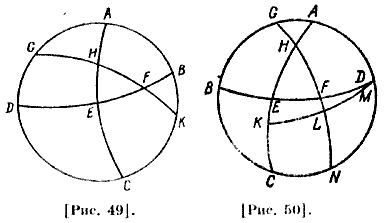
Существует более легкий, чем этот, способ определения угла, образуемого наклонным кругом и [большим кругом] , проходящим через зенит, и дуг, взятых в этом круге, когда известны [величины] углов и дуг в меридиане или в круге горизонта. Пусть сначала требуется определить угол, расположенный между ними, то есть между [кругом], проходящим через зенит, и косым [кругом] в отношении горизонта.

Пример этого. Пусть ABCD — меридиан [рис. 48], BED — горизонт, А — зенит, [то есть] полюс горизонта, GEH — данная дуга наклонного [круга]; высота полюса 36 градусов. Если G — точка в середине неба, то круг ABC будет тем же кругом зенита, проходящим через G. Поскольку точка G, дана, то угол G известен; AG известна.

Пусть проведем круг АЕС через восходящую точку Ε и полюс [горизонта] А, тогда дуга АЕ будет равна четверти круга. Поэтому угол AED будет прямым, а угол, образуемый пересечением косого [круга] и горизонта, то есть ВЕН, известен, следовательно, весь угол АЕН известен; поэтому дуги, стягивающие эти углы, известны.

Точно так же если будет известно расстояние между точкой и меридианом, то [прямые] часы, то есть дуга параллельных кругов, будут известны. Пусть точка G на меридиане заменяет точку Н, которая представляет начало Рака [рис. 49], и пусть оно отстоит к востоку от меридиана по дуге параллели на один прямой час. Точка будет известной по сказанному выше. Точка воcхождения известна. Проведем через А и Η круг зенита до Ε и С; дуга FHG известна, HF известна; AG по сказанному выше известна; дуга DG — остаток от четверти [круга] известна; тогда дуга BG известна. Отношение синуса известной GB к синусу известной АВ составлено из отношения синуса известной АЕ к синусу неизвестной ЕН и синуса известной FH к синусу известной FG. Отсюда определим ЕА и АН и, следовательно, дугу зенита.

Если хотим определить угол AHF, то пусть вокруг полюса Η 34 на расстоянии, равном стороне [вписанного] квадрата, опишем отрезок KLM большего круга [рис. 50]. Поскольку дуга АЕС

проходит через полюсы кругов EFM и KLM, то каждая из ЕМ и КМ равна четверти круга. Отношение синуса известной ЕН к синусу известной ЕК (так как ЕК остаток от четверти [круга]) составлено из отношения синуса известной HF к синусу известной FL и из отношения синуса неизвестной ML к синусу известной КМ, становится известной ML и, следовательно, оставшаяся LK будет известной. Поэтому известны углы KHL и AHF.

Точно так же вычисляются [места] точек одно за другим.

Затем он составил таблицу по этому же способу и для каждого климата⁹³. Она начинается с параллели, проходящей через остров Мероэ, где наибольший день равняется тринадцати прямым часам и продолжается с приращением по полчаса до [параллели], где наибольший день равняется шести. Он взял [для дуг эклиптики приращения] по одному знаку, для широты — по полчаса, для положения [кругов к западу и востоку] от середины неба — по одному [прямому] часу. В первом столбце поместил числа, [выраженные] в прямых часах расстояний от меридиана, когда эклиптика наклонна к меридиану; во втором столбце — величины дуг между наклонным кругом и зенитом; в третьем столбце — величины углов у [каждого рассматриваемого] сечения [для положений] к востоку, а в четвертом — западных [углов]. При этом он отмечает, что в первом случае берутся углы к северу от сечения и прямой угол содержит девяносто градусов.

Что касается стран, их широт и долгот, то он обещал создать отдельную книгу и [позднее] написал свое сочинение «География»⁹⁴. Помощь от Аллаха!

Комментарии

62. Вторая книга «Альмагеста» Птолемея состоит из следующих глав:

О положении обитаемой нами Земли вообще.

О том, как по заданной величине наибольшего дня определяются дуги горизонта, отсекаемые равноденственным и косым кругом.

О том, как при тех же предположениях определяется высота полюса.

О том, как вычисляется, где, когда и сколько раз Солнце бывает прямо над головой.

О том, как на основании изложенного определяются отношения гномонов к полуденным теням во времена равноденствий и солнцеворотов.

Перечень характерных особенностей для отдельных параллелей.

Об одновременных выхождениях на наклонной сфере частей кругов — проходящего через середины зодиакальных созвездий и равноденственного.

Таблица восхождений по дугам в десять градусов.

О частных вопросах, связанных с восходами.

Об углах, образуемых проходящим через середины зодиакальных созвездий и полученным кругами.

Об углах, образуемых тем же косым кругом с горизонтом.

Об углах и дугах, образуемых тем же кругом с проведенным через полюс горизонтом.

Значения упомянутых углов и дуг для различных параллелей.

63. Аль-Фараби иногда „Комментарии к «Альмагесту»" называет „Сокращением «Альмагеста»".

64. В начале второй книги «Альмагеста» Птолемей пишет: «После того, как в первой книге этого сочинения мы изложили вкратце необходимые сведения относительно положения Вселенной, а также все относящееся к прямой сфере и считаемое полезным для теоретического рассмотрения предложенного, мы попытаемся в дальнейшем изложить все, что происходит на наклонной сфере, опять излагая наиболее существенное и насколько возможно понятное». [3, стр. 58].

65. Аль-Фараби, по-видимому, несколько отходя от Птолемея, предполагает, что обитаемы те места, где во время равноденствий тени направлены не только к югу, но и к северу.

66. Аль-Фараби рассматривает способы определения широты (φ) обитаемых частей Земли, которая измеряется высотой полюса над горизонтом, что отсутствует в «Альмагесте».

Если h_max и h_min — соответственно наибольшая и наименьшая высоты не заходящих звезд, то, по аль-Фараби,

67. Это правило аль-Фараби, которого также нет в «Альмагесте», соответствует формуле:

где h₁ и h₂ — высоты Солнца в истинный полдень в дни летнего и зимнего солнцестояний.

68. Азимут восхода (са'ат аль-машрик), этот термин отсутствует в «Альмагесте». Восточные математики под этим понимали дугу горизонта от точки Солнца в данный день до точки востока.

69. Здесь фактически установлено следующее соотношение:

70. Здесь фактически установлено следующее соотношение:

71. Здесь фактически установлено следующее соотношение:

Полученное выражение дуги FE в градусах при переводе в часы делится на 15.

72. Доказано другое соотношение

для определения азимута восхода ЕН:

73. Аль-Фараби пропустил главу «Альмагеста» о том, как вычисляется, где, когда и сколько раз Солнце бывает прямо над головой, где говорится: «При помощи вышеприведенных данных легко вычислять, где, когда и сколько раз Солнце бывает прямо над головой. Действительно, непосредственно очевидно, что для точек, находящихся на параллелях, отстоящих от равноденственного круга далее, чем все расстояние точки летнего солнцеворота, т. е. приблизительно 23; 51,20 градусов, Солнце никогда не будет прямо над головой, для точек, находящихся как раз на таком расстоянии, оно будет только один раз во время самого летнего солнцеворота, а для точек, лежащих на расстоянии, меньшем указанного числа градусов, Солнце два раза окажется прямо над головой; соответствующее время легко получается по приведенной выше таблице склонений. Действительно, взяв во втором столбце таблицы число градусов, на которое рассматриваемая параллель отстоит от равноденственного круга (конечно, внутри летнего тропика), мы получим в соответствующем месте первого столбца число градусов первого квадранта, показывающее, на сколько Солнце отстоит от каждой из равноденственных точек по направлению к точке летнего солнцеворота, когда оно становится прямо над головой для точек, лежащих на указанной параллели» [3, стр. 65—66]. Но этот материал аль-Фараби вкратце излагает в главе «Об особенностях кругов, параллельных небесному экватору».

74. Гномон (микийас), шест, разделенный на определенное количество (здесь на 60) частей, по тени которого определялись время, высота и азимут Солнца и ряд других данных. Греческое слово gnomon означает «указатель». Гномоны чаще всего устанавливались вертикально на горизонтальной плоскости и горизонтально на вертикальной стене.

75. Аль-Фараби вносит существенное дополнение к рассуждениям и рисунку Птолемея.

76. В этой главе аль-Фараби, следуя Птолемею, кратко резюмирует материал, касающийся разделения земной поверхности на «климаты» в зависимости от продолжительности наибольшего дня.

Климаты (арабское — «иклим») — широтно-климатические зоны по астрономо-географическому принципу, принятому в античности, по которому обитаемые части земной поверхности делились в соответствии с продолжительностью дня летнего солнцестояния или величиной склонения Солнца.

Впервые деление ойкумены на семь «климатов» по широтному принципу встречается у аль-Хорезми. Позднее аль-Бируни в своих сочинениях руководствуется этим и другими принципами.

77. По-видимому, здесь аль-Фараби считает возможной обитаемость этой параллели, что обсуждалось в упоминаемом им сочинении «Естествознание». Отметим, что в своих естественнонаучных сочинениях Аристотель также предполагал о существовании на юге экватора земель, близких по своим климатическим условиям к землям северного полушария. Впоследствии аль-Бируни также полагал, что «обитаемые [земли] не оканчиваются сразу же за пределами седьмого климата или перед началом первого, но они сокращаются и идут отдельными обособленными пятнами» [9, стр.193].

78. «География» (Джаграфиус)—сочинение Птолемея в восьми книгах, основу которого составляют таблицы географических координат населенных пунктов и карты Земли. Судя по неоднократным ссылкам, содержание этого трактата было хорошо известно аль-Фараби.

79. В «Альмагесте» — «неизвестные скифские племена».

80. Теоретические соображения, приведенные в этом абзаце, отсутствуют в «Альмагесте» и служат для понимания дальнейших рассуждений Птолемея относительно явлений, наблюдаемых в более высоких широтах.

81. Эта глава в «Альмагесте» начинается так: «После изложения того, что вообще наблюдается на различных климатах, нам следовало бы показать, как для каждого климата определяются одновременно восходящие часовые градусы равноденственного круга и соответствующие дуги зодиакального; отсюда нами будут последовательно выведены и все остальные подробности.

Мы будем пользоваться названиями знаков Зодиака и для обозначения соответствующих им двенадцати равноденственных и солнцеворотных точек; первую двенадцатую часть, начинающуюся от точки весеннего равноденствия и идущую в направлении мирового движения, мы будем называть Овном, вторую — Тельцом и так далее, согласно установленной последовательности 12 зодиакальных созвездий.

Покажем сначала, что равные дуги зодиакального круга, начинающиеся от одной и той же равноденственной точки, будут всегда одновременно восходить с равными же кругами равноденственного круга» [3, стр. 21].

82. Доказанное правило для нахождения значений местного восхождения αφ градуса точек эклиптики сводится к формуле

где α — прямое восхождение градусов эклиптики, Δα — «уравнение дня».

Уравнение дня — дуга небесного экватора от пересечения его большим кругом, проходящим из полюса мира через точку восхода светила до точки востока (дуга ЕМ), или же дуга суточной параллели от пересечения последней большим кругом, проходящим из полюса через точку, до точки восхода светила. Этот термин отсутствует в «Альмагесте».

83. Здесь доказывается правило, равносильное соотношению:

где FE — выражение в градусах половины разности между наибольшим и наименьшим днями;

с другой стороны, по доказанному выше

Из этих соотношений получается та же формула для нахождения восхождений градуса эклиптики:

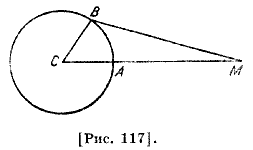
84. Птолемей, производя подробные вычисления значений одновременных восхождений градусов эклиптики (через 10 градусов) для параллели, проходящей через остров Родос (широта, т. е. высота полюса 36 градусов, наибольший день 14,5 часа), далее пишет: «Итак, вычислив таким же образом восхождения для каждых десяти градусов и на остальных параллелях, чтобы быть готовыми ко всякого рода практическим приложениям, мы приведем их в таблицах для использования в дальнейшем, начиная с самого равноденственного круга и до параллели с наибольшим днем в 17 часов, давая приращения по полчаса, так как в пределах получаса разности несущественно отличаются от получающихся при равномерном изменении. Поставив 36 десятиградусных делений круга, для каждого дадим ниже и временные градусы восхождений для соответствующего климата и величины, получаемые при их сложении» [3, стр. 93].

85. Аль-Фараби не приводит утомительные для читателей вычислительные выкладки для нахождений числовых значений восхождений точек эклиптики и сразу указывает на готовые таблицы восхождений по дугам в десять градусов.

Эта таблица приведена нами в приложениях (таблица 3).

86. Начало этой главы в «Альмагесте» выглядит так: «После того, как мы приведенным выше образом показали времена восхождений, то все остальное, относящееся к этому предмету, делается легко понятным и нам не понадобятся ни геометрические доказательства каждого из этих сведений, ни составление излишних таблиц, но общий ход рассуждения будет вполне ясным при помощи только приведенных выше таблиц» [3, стр. 93].

87. Сезонный или косой час — 1/12 продолжительности соответствующего

дня или ночи. Ввиду неравенства этих дуг (кроме дней равноденствия) сезонный час ночи не равен сезонному часу дня.

88. Градусы времени, или временные градусы, — градусы небесного экватора.

89. Равноденственные (равновеликие), или прямые часы, — часы в нашем употреблении, т. е. 1/24 средних суток.

90. Параллакс — ихтилаф манзар — «различие видения» — угол между прямыми линиями, соединяющими светило с наблюдателями, находящимися в диаметрально противоположных точках земного шара (суточный параллакс) или в диаметрально противоположных точках земной орбиты (годичный параллакс). Особое значение для практической астрономии имеет параллакс Луны. Если Μ означает Луну [рис. 117], С — центр Земли, А — точку на земной поверхности, где Луна стоит над головой наблюдателя, а В — другую точку земной поверхности, то наблюдатели, находящиеся в А или В, одновременно видят Луну вдоль линий СМ и ВЫ, разница направлений между которыми измеряется углом ВМС, носящим название параллакса и зависящим от расстояния Луны и положения наблюдателя.

91. Сторона квадрата, вписанного в большой круг сферы, — раствор циркуля, которым описываются на поверхности сферы ее большие круги. Такой большой круг, описанный из точки пересечения двух больших кругов, является их общим перпендикуляром. Угол между двумя пересекающимися большими кругами сферы равен расстоянию между ними по этому большому кругу.

92. Колышек Земли (ватад) — место пересечения эклиптики с полуночным кругом, соответствующим полуденному кругу. В Европе «Колышки» назывались cardines или puncta cardinalis — «кардинальные точки» — точки пересечения эклиптики с меридианом и горизонтом. Верхний из них называется «колышком середины неба» («середина неба» — небесный меридиан), нижний — «колышком Земли».

93. Эта таблица приведена в приложениях нашей работы (таблица 4).

94. В «Альмагесте» почти не приводятся сведения, касающиеся географии стран света, в том числе координатов местностей; эти материалы даны в «Географии» Птолемея.